問題
△OABのOA.OB上にそれぞれ点C,Dをとり、ADとBCの交点をP とする。
また、2点Q,Rを四角形OCQD、四角形OARBがそれぞれ平行四辺形となるようにとると、
3点P,Q,Rは一直線上であることを証明せよ。
解答(太字はベクトルです)
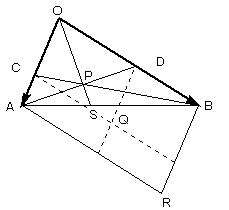
OA=a、OB=b とおき、OC=sa、OD=tb (ただし、0<s<1,0<t<1) とおきます。
つまり、OC:CA=s:(1−s)、 OD:DB=t:(1−t) です。
チェバの定理より、
(AS/SB)(DB/OD)(OC/CA)=1
(AS/SB){(1−t)/t}{s/(1−s)}=1
よって、
AS:SB=(1−s)t:(1−t)s=(t−st):(s−st)
一方、メネラウスの定理より
(OP/PS)(SB/AB)(AC/CO)=1
(OP/PS){(s−st)/(s+t−2st)}{(1−s)/s}=1
より、
OP:PS=(s+t−2st):(1−s)(1−t)
つまり、
OP:OS=(s+t−2st):(1−st)
よって、
OS={(s−st)a+(t−st)b}/(s+t−2st)
OP=(s+t−2st)OS/(1−st)
={(s−st)a+(t−st)b}/(1−st)
また、
OQ=sa+tb
OR=a+b
以上から
PR=OR−OP
={(1−s)a+(1−t)b}/(1−st)
QR=OR−OQ
=(1−s)a+(1−t)b
よって、
PR=QR/(1−st)
となり、P,Q,R は一直線上にあることになります。
算数・数学の部屋に戻る