問題
(1) 四角形OABCは平行四辺形で、2点A、Dは関数y=x2/4 (x>0) のグラフ上にある。
点Oは原点で、点Cの座標は(3、6)、点Dの座標は8である。
平行四辺形OABCの面積が6の時、点Aの座標を求めよ。
ただし、点Aの座標は 3<x<8の範囲にあるものとする。
(2) 関数y=x2/2のグラフ上に、4点A(−2、2)、B(4、8)、C、Dがあり、
四角形ABCDはAB//DC、AB:DC=3:2となる台形である。
線分ADに平行な直線Lが台形ABCDの面積を2等分するとき、Lの式を求めよ。
解答
(1) 点Dについての情報はこの際無関係なので、無視します。
点Aの座標を(t、t2/4)と置きます。ただし、3<t<8。
平行四辺形の面積の公式を利用して、
OA=(t、t2/4)、OC=(3,6) より、平行四辺形OABCの面積を出すと、
|t・6−(t2/4)・3|=6
両辺4/3を掛けて
|8t−t2|=8
0<t<8 の範囲で 8t−t2>0なので、絶対値記号をはずして
8t−t2=8
これを解いて、
t=4±2√2
3<t<8 より、
t=4+2√2
このとき、
t2/4=6+4√2
答え:(4+2√2、6+4√2)
(2)
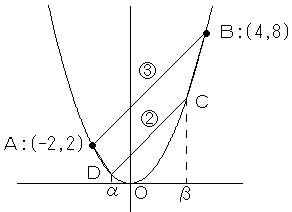
まず、点Dの座標を求めます。
直線ABの傾きは1なので、直線CDの傾きも1です。
一方、点Aと点Bのx座標の差が6なので、点Cと点Dのx座標の差は4です。(AB:CD=3:2 より)
上図のように、点Cのx座標をβ、点Dのx座標をα(α<β)とすると、
β−α=4
直線CDの式を
y=x+m
とおく。これと、
y=x2/2
との連立方程式の解が2点C、Dになる。2式よりyを消去して、
x2/2=x+m
x2−2x−2m=0
これの解がα、βとなります。
解と係数の関係より、
α+β=2、αβ=−2m
一方、
(β−α)2=(α+β)2−4αβ=4+8m=16
m=3/2
よって、x2−2x−2m=0 に代入した
x2−2x−3=0
を解いて、
x=−1,3
よって、点Dの座標は(−1,1/2) となります。
直線ADの傾きは、-3/2 です。
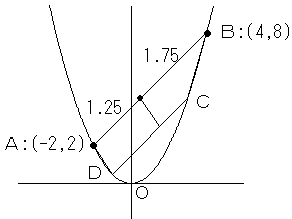
上底2,下底3の台形の面積は、高さが同じで、底辺2.5の平行四辺形の面積と同じです。
つまり、台形ABCDをADに平行な直線で二等分するには、ABを 1.25:1.75 に内分する点を
通るようにすればよい。
1.25:1.75=5:7
より、求める点は、(1/2、9/2)
よって、Lの式は、
y−9/2=-3/2(x−1/2)
変形して、
6x+4y=21・・・答え
「算数・数学」の部屋に戻る