これを応用して、xy平面上での2つのベクトル
a=(xa、ya)、b=(xb、yb)
で形成される平行四辺形の面積は、|xayb−xbya| で表される。
とくにaとbの位置関係によって、絶対値内の正負を下図のように決定できる。
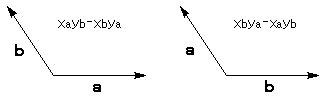
※この公式は、以下のような図からも導けます。
ベクトルの向きによって、いろいろな形になりますが、すべて同じ結果になります。
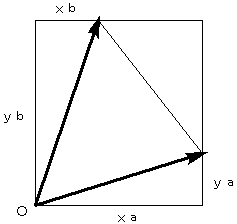
ベクトルの外積
2つのベクトル
a=(xa、ya、za)、b=(xb、yb、zb)
に対して、aとbの外積a×bを以下のように定義する。
a×b=(yazb−ybza、zaxb−zbxa、xayb−xbya)
c=a×b、d=b×a とするとき、以下の性質がある。
1.c・a=0、c・b=0
2.c=−d
3.cの向きは、aをbに向けて、180°より小さい方の角の方向に回転させたとき、
右ネジの進む方向に向く。
aとbの角が0°または180°のときは、c=0となるので、向きは考慮外である。
4.|c| は、aとbとで作られる平行四辺形の面積に等しい。
応用:平行四辺形の面積
これを応用して、xy平面上での2つのベクトル
a=(xa、ya)、b=(xb、yb)
で形成される平行四辺形の面積は、|xayb−xbya| で表される。
とくにaとbの位置関係によって、絶対値内の正負を下図のように決定できる。
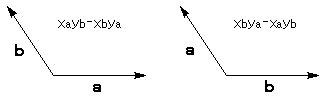
※この公式は、以下のような図からも導けます。
ベクトルの向きによって、いろいろな形になりますが、すべて同じ結果になります。
