数列 a, b, c, a2, ab, ac, b2, bc, c2, a3, a2b, a2c, ab2, abc, ac2, b3, b2c, bc2, c3, A4, a3b, a3c, …
(同次では辞書式の順)において、
(1) n次の項は何項あるか。
(2) akb2は第何項か。
解答1
(1)例えば、3次の項は次のように考えます。
○○○||
のように、3つの○と2本の|を、いろいろな順番に並べます。
○○○||
○○|○|
○○||○
○|○○|
○|○|○
○||○○
|○○○|
|○○|○
|○|○○
||○○○
の10通りがあります。
求め方は 5!/(3!×2!) です。
|で仕切られた3つの部分をそれぞれ
(aの次数)|(bの次数)|(cの次数)
と見なし、○の数が次数(○がないときはその文字はない)を表していると考えると、
上の図は、上から順に、
a3, a2b, a2c, ab2, abc, ac2, b3, b2c, bc2, c3
を表しています。
一般に、n次の項であれば、n個の○と2本の|の並べ方なので、
(n+2)!/(n!×2!)=(n+2)(n+1)/2
となります。
一般にn種類のものからm個のものを取るやり方は
重複組み合わせと言って、nHm で表します。
nHm=n+m-1Cm
の関係があります。
(2) akb2は、k+2次の項の4番目の項です。
まず、1次からk+1次までに、いくつ項があるかを調べます。
(n+2)(n+1)/2 を n=1〜k+1まで足すと、
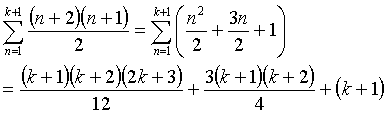
となり、整理すると、
(k+1)(k2+8K+18)/6 数列の和参照
これに4を足して、
(k+1)(k2+8K+18)/6+4
または
(k3+9k2+26k+42)/6
問題2
自然数の列A1、A2、A3、A4、A5は等比数列であるとし、
S=A1+A2+A3+A4+A5
S'=A1-A2+A3-A4+A5
T=A12+A22+A32+A42+A52
とおく。
(1)整数Tは整数Sで割り切れ,その商はS’となることを示せ。
(2)Tが素数となる場合のTの値を求めよ。
解答2
A1=a, A2=ar, A3=ar2, A4=ar3, A5=ar4
とおく。ただし、a, r はともに自然数。
また一般に
An-rAn+r=An2 ただし 0≦r<n
(1)S>0 なので、
T=SS’
を示せばよい。
SS’=(A1+A3+A5)2-(A2+A4)2
=A12+A32+A52+2A3A5+2A5A1+2A1A3-A22-A42-2A2A4
=A12+A32+A52+2A42+2A32+2A22-A22-A42-2A32
=A12+A22+A32+A42+A52 = T
以上より、TはSで割り切れ、その商はS’である。
(2)Tが素数ならば、
T=SS’ および S>S’より、
S=T S’=1
一般にnが自然数のとき、
n≦n2
であり、等号は n=1 のときに成り立つ。いま、
A1≦A12
A2≦A22
A3≦A32
A4≦A42
A5≦A52
を、辺々加えて、
S≦T
ただし等号は、A1=A2=A3=A4=A5=1 のときに成り立つ。
よって、S=T のとき、
S=T=5
答え:T=5
「算数・数学」の部屋に戻る