5.純正律
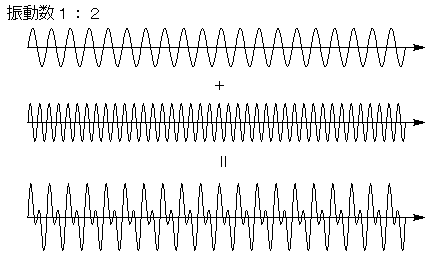
第4章で、振動数比が整数比であるとハモるということを説明しました。
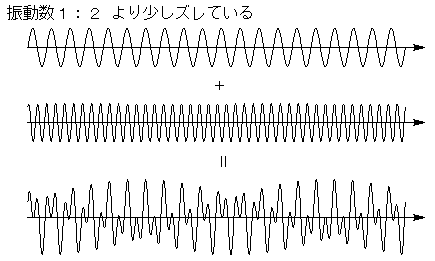
一方、整数比に近くても、少しズレていれば、やはりうなりが生じます。
A音440Hz に対して、振動数比 2:3 にあたる振動数は 660Hz です。
平均律で、この振動数に近い音は、E音(440×27/12=659.255Hz) です。
ところが、これは660Hzより、少し低いので、ハモらせるためには、平均律より
少し高めに修正しないといけません。その量をセントで計算すると、
1200×log2(1.5/27/12)=1.95500 (セント)
となります。
半音7つ分(3全音半)の開きがある音程を、完全5度と言います。
CとG、EとB、FとC などが完全5度です。
| 完全5度は上の音を平均律より 約2セント高めにするとハモる |
A音440Hz に対して、振動数比 4:5 にあたる振動数は 550Hz です。
平均律で、この振動数に近い音は、C#音(440×24/12=554.365Hz) です。
ところが、これは550Hzより、かなり高いので、ハモらせるためには、平均律より
かなり低めに修正しないといけません。その量をセントで計算すると、
1200×log2(1.25/24/12)=-13.686 (セント)
となります。
半音4つ分(2全音)の開きがある音程を、長3度と言います。
CとE、EとG#、FとA などが長3度です。
| 長3度は上の音を平均律より 約14セント低めにするとハモる |
A音440Hz に対して、振動数比 5:6 にあたる振動数は 528Hz です。
平均律で、この振動数に近い音は、C音(440×23/12=523.251Hz) です。
ところが、これは528Hzより、かなり低いので、ハモらせるためには、平均律より
かなり高めに修正しないといけません。その量をセントで計算すると、
1200×log2(1.2/23/12)=15.641 (セント)
となります。
半音3つ分(1全音半)の開きがある音程を、短3度と言います。
CとE♭、EとG、FとA♭ などが短3度です。
| 短3度は上の音を平均律より 約16セント高めにするとハモる |
ある3音P、Q、Rの音程が、
P←長3度→Q
Q←短3度→R
P←完全5度→R (上2つが決まれば、自動的に完全5度になります)
の関係にある和音を、長3和音と言います。
自然長音階では ドミソ、ファラド、ソシレ が長3和音です。
長3和音では、上記の規則に従い、真ん中の音を14セント下げ、上の音を2セント上げるとハモります。
ある3音P、Q、Rの音程が、
P←短3度→Q
Q←長3度→R
P←完全5度→R (上2つが決まれば、自動的に完全5度になります)
の関係にある和音を、短3和音と言います。
自然長音階では レファラ、ミソシ、ラドミ が短3和音です。
短3和音では、上記の規則に従い、真ん中の音を16セント上げ、上の音を2セント上げるとハモります。
このように、振動数比が整数になるように、平均律から少しずつ修正した音律(各音の音程の決め方)を、
純正律といいます。
| |
平均律 |
純正律 |
| 長所 |
転調が自由に出来る |
ハモった状態を作れる |
| 短所 |
完全にハモった響きは得られない |
調により、音程が変わる
ハモれない和音もある(純正律固定された楽器の場合) |
| 楽器 |
多くの鍵盤(打)楽器、ギターなど |
多くの管楽器、バイオリンなど |
完全5度は2セントの差なので、ほとんど問題にされませんが、
長短3度は、意識して変化させないと、ハモらせることが出来ません。
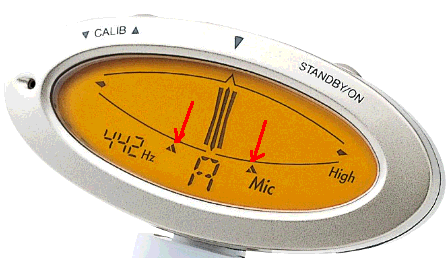
最近のチューナーは、-14セント、+16セントの所に印の付いているものが多い。

4.うなりとハモり へ
6.半音階の純正律 へ



