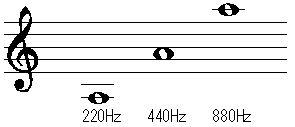2.オクターブと完全5度から平均律へ
振動数が 1:2 の関係にある2つの音を、完全8度(オクターブ)と言います。
440Hz のA音に対して、1オクターブ下、1オクターブ上のA音の振動数は、
それぞれ、220Hz、880Hz です。
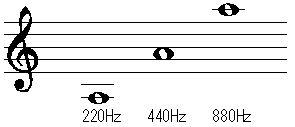
1オクターブで、振動数2倍、2オクターブで振動数4倍、3オクターブで振動数8倍となります。
振動数が 1:2 の完全8度とともに、振動数が2:3 の完全5度の存在も、
心地よく響く音程として、昔から知られていました。
そこで、振動数を1.5倍する(完全5度上げる)、または0.5倍する(1オクターブ下げる)
ことを繰り返しすと、12回で、元の音に近い振動数になります。
表1(音名はその振動数に近い音を当てはめたものです)
| 音名(英) |
A |
E |
B |
F# |
C# |
G# |
D# |
A# |
F |
C |
G |
D |
A? |
| 振動数 |
440 |
660 |
990 |
743 |
1114 |
835 |
1253 |
940 |
705 |
1057 |
793 |
1189 |
892 |
1オクターブ
下の振動数 |
|
|
495 |
|
557 |
|
626 |
470 |
|
529 |
|
595 |
446 |
これを、音名順に並べると、
表2
| 音名 |
A |
A# |
B |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
| 振動数 |
440 |
470 |
495 |
529 |
557 |
595 |
626 |
660 |
705 |
743 |
793 |
835 |
892 |
となります。
さて、音の間隔(音程)は、振動数比によって決まります。
X(440Hz)、Y(470Hz)、Z(500Hz)
の3つの音があるとします。XとY、YとZ の振動数の差はいずれも30Hz ですが、
これら2組の音のペアは、同じ音程には、聞こえません。
一方、
L(440Hz)、M(660Hz)、N(990Hz)
において、LとM、MとNの、振動数の比は、いずれも 2:3 です。
これら2組の音のペアは、同じ音程に聞こえます。
上の L、M、N の例では、
MはLの1.5倍
NはMの1.5倍
NはLの1.52倍
の振動数になっています。以下、Lの振動数の
1.53倍、1.54倍、1.55倍 ・・・
の音を連ねると、隣り合う2音の音程が同じ音列を作ることが出来ます。
同様にして、隣り合う2音の音程が同じ音列を作り、12回目で、1オクターブ(振動数が2倍)
にするには、隣り合う2音間の振動数比を、いくらにすればいいでしょうか?

一番下の音の振動数を f 、求める振動数比を r(r>1) とすると、音列の振動数は
f、fr、fr2、fr3、fr4 ・・・ fr12
となります。fr12 が f の2倍の振動数になればいいので、
r12=2
r=12√2=1.05946309・・・
この振動数比で、表2の振動数を計算すると
表3:平均律の振動数
| 音名 |
A |
A# |
B |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
| 振動数 |
440 |
466 |
494 |
523 |
554 |
587 |
622 |
659 |
698 |
739 |
783 |
830 |
880 |
となります。これらの音列は、どの隣り合った2音をとっても、同じ音程であり、
また、同じ間隔どうしの2音(例えば、間を2つ空けて取った任意の2音)は、
どれも同じ音程になります。例えば、
AとC、A#とC#、BとD などはすべて同じ音程です。
このように、1オクターブを均等に12に分けて決めた音程を平均律といいます。
また、表3で隣り合った2音の音程を半音、半音2つ分の音程を全音といいます。
| 平均律の半音の振動数比は 21/12=1.05946309・・・ |
1.振動数 へ
3.セント へ