問題
四面体OABCにおいて、線分OAを1:2に内分する点をP,線分OBを1:3に内分する点をQ,線分OCを1:4に内分する点をRとする。
(1) 2点P,Qを通る直線と、2点A,Bを通る直線との交点をTとするとき、
OT=□OA+□OB+□OC
である。
(2) 2点Q,Rを通る直線と、2点B,Cを通る直線との交点をUとすると
OU=□OA+□OB+□OCである。
(3) △ABCの面積は△TBCの何倍か?また△TUBの面積の何倍か?
解答
(1)
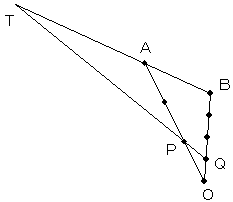
解法1
メネラウスの定理より、
(AP/PO)(QB/OQ)(BT/TA)=1
BT/TA=3/2
よって、AT:AB=2:1
OT=OA+AT
=OA+2BA
=OA+2(OA−OB)
=3OA−2OB
解法2
TはAB上にあるので、
OT=(1−s)OA+sOB (sは実数)
TはPQ上にあるので、
OT=(1−t)OP+tOQ
=(1−t)OA/3+tOB/4 (tは実数)
とそれぞれおけます。OAとOBは平行でないので、
1−s=(1−t)/3
s=t/4
これを解いて、s=−2、t=−8。よって、
OT=3OA−2OB
答え OT=3OA−2OB+0OC
(2)
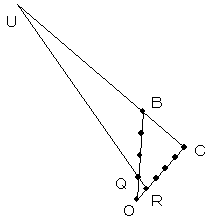
解法1
メネラウスの定理より、
(CU/BU)(QB/OQ)(OR/RC)=1
CU/BU=4/3
よって、BU:BC=3:1
OU=OB+BU
=OB+3CB
=OB+3(OB−OC)
=4OB−3OC
解法2
UはBC上にあるので、
OU=(1−s)OB+sOC (sは実数)
UはQR上にあるので、
OU=(1−t)OQ+tOR
=(1−t)OQ/4+tOR/5 (tは実数)
とそれぞれおけます。OAとOBは平行でないので、
1−s=(1−t)/4
s=t/5
これを解いて、s=−3、t=−15。よって、
OU=4OB−3OC
答え OU=0OA+4OB−3OC
(3)
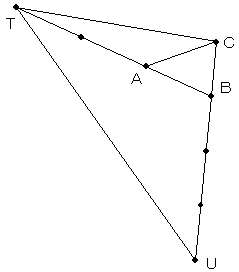
メネラウスの定理を使った場合は、
BT:AB=3:1
BU:BC=3:1
であることがわかっています。そうでないときは、
AT=OT−OA=2(OA−OB)=2BA
BU=OU−OB=3(OB−OC)=3CB
より、上記の比が求まります。以上より、
△ABCは、△TBCの1/3倍、△TUBの1/9倍 とわかります。
「算数・数学」の部屋に戻る