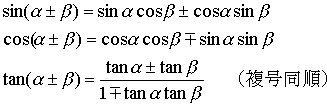
2倍角の公式
三角関数の加法定理
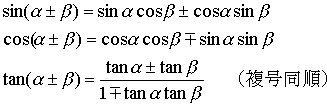
2倍角の公式
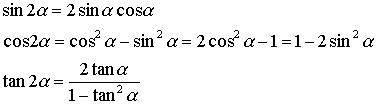
(証明)
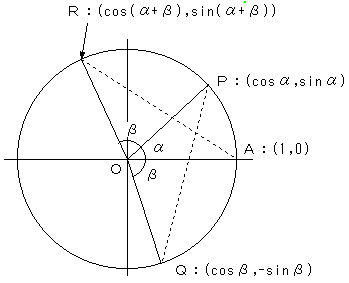
図のように、単位円上に、4点 A,P,Q,R
をとります。このとき
AR2={cos(α+β)−1}2+{sin(α+β)−0}2
=cos2(α+β)−2cos(α+β)+1+sin2(α+β)
=2−2cos(α+β)
PQ2=(cosα−cosβ)2+(sinα+sinβ)2
=cos2α−2cosαcosβ+cos2β+sin2α+2sinαsinβ+sin2β
=2−2(cosαcosβ−sinαsinβ)
となります。AR2=PQ2 より、
cos(α+β)=cosαcosβ−sinαsinβ
を得ます。また β を −β に置き換えると、
cos(α−β)=cosαcosβ+sinαsinβ
を得ます。一方、
sinA=cos(90°−A)
より、
sin(α+β)=cos{90°−(α+β)}=cos{(90°−α)−β}
=cos(90°−α)cosβ+sin(90°−α)sinβ
=sinαcosβ+cosαsinβ
を得ます。β を −β に置き換えると、
sin(α−β)=sinαcosβ−cosαsinβ
を得ます。
tanA=sinA/cosA
より、
tan(α+β)=sin(α+β)/cos(α+β)
=(sinαcosβ+cosαsinβ)/(cosαcosβ−sinαsinβ)
分母子を cosαcosβ で割って,
tan(α+β)=(tanα+tanβ)/(1−tanαtanβ)
を得ます。β を −β に置き換えると
tan(α+β)=(tanα−tanβ)/(1+tanαtanβ)
を得ます。
また、加法定理の公式において、β=α とおくと、2倍角の公式が得られます。
以上
「算数・数学の部屋」に戻る