三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、
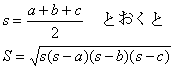
と表せる。
ヘロンの公式(代数的証明)幾何的証明はこちら
三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、
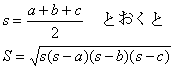
と表せる。
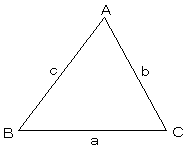 |
以下の説明では、左図のように、頂点および角度をA,B,Cで表し 各頂点に向かい合う辺の長さを、a,b,c で表します。 |
証明
使用する公式
・三角関数の基本公式
sin2A+cos2A=1
・余弦定理
a2=b2+c2-2bccosA
b2=c2+a2-2cacosB
c2=a2+b2-2abcosC
・三角形の面積の公式(面積をSとする)
![]()
余弦定理の第1式より
![]() ・・・(1)
・・・(1)
sin2A+cos2A=1 において、0<A<π より sinA>0
よって、
![]()
(1) を代入して、
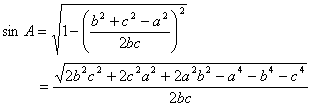
よって、三角形の面積Sは
![]()
一方、ヘロンの公式の右辺は、
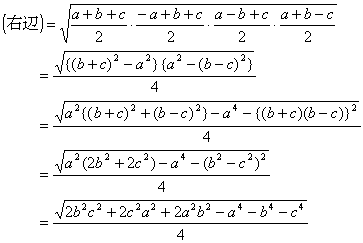
以上より、ヘロンの公式で、三角形の面積が求められることが分かる。
「算数・数学の部屋」に戻る