問題
各位の数がすべて素数であるようなｎ桁の自然数Ｎについて考える。
各位の数の和が奇数となるようなＮの個数を求めよ。
解答
漸化式と特性方程式もあわせてご覧ください。
各位の数がすべて素数であるようなｎ桁の自然数Ｎで、各位の数の和が
奇数である数の個数を ａn
偶数である数の個数を ｂn
とします。ここで、ａ1＝３（３と５と７）、ｂ1＝１（２のみ） です。
各位の数がすべて素数であるようなｎ桁の自然数の右に２，３，５，７ のいずれかを付けて
ｎ＋１桁の数を作ることを考えます。
ａn個のｎ桁の数に、２が付くと、和は奇数のままなので、ａn+1 の一部になります。
ａn個のｎ桁の数に、３，５，７のいずれかが付くと、和は偶数になり、ｂn+1 の一部になります。
ｂn個のｎ桁の数に、２が付くと、和は偶数のままなので、ｂn+1 の一部になります。
ｂn個のｎ桁の数に、３，５，７のいずれかが付くと、和は奇数になり、ａn+1 の一部になります。
以上より、
ａn+1＝ａn＋３ｂn
ｂn+1＝３ａn＋ｂn
という漸化式が出来ます。これを行列で書くと、
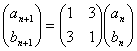
と書けます。（ａ1 ｂ1）t からたどっていくと、
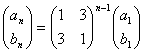・・・(1)と書けます。
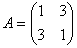とおくと、ケーリー・ハミルトンの公式より
Ａ2−(1+1)Ａ＋(1・1−3・3)Ｅ＝Ｏ
Ａ2−２Ａ−８Ｅ＝Ｏ
Ａn を掛けて、
Ａn+2−２Ａn+1−８Ａn＝Ｏ
右から（ａ1 ｂ1）t を掛けて、
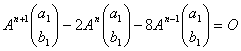
(1) より、
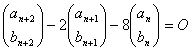
これより、
ａn+2＝２ａn+1＋８ａn
ｂn+2＝２ｂn+1＋８ｂn
という、漸化式が出来ます。ただし、ａ1＝３、ａ2＝６、ｂ1＝１、ｂ2＝10
ａn+2＝２ａn+1＋８ａn
より、
ａn+2−４ａn+1＝−２(ａn+1−４ａn)
と変形出来ます。ｃn＝ａn+1−４ａn とおくと、ｃn+1＝−２ｃn および、ｃ1＝ａ2−４ａ1＝−６ より、
ｃn＝３(-2)n
と書けます。同様に、ｄn＝ｂn+1−４ｂn とおくと、ｄn+1＝−２ｄn および、ｄ1＝ｂ2−４ｂ1＝６ より、
ｄn＝-３(-2)n
と書けます。
ａn+1−４ａn＝３(-2)n
ｂn+1−４ｂn＝-３(-2)n
より、
ａn+1+(1/2)(-2)n+1＝４{ａn+(1/2)(-2)n}
ｂn+1-(1/2)(-2)n+1＝４{ｂn-(1/2)(-2)n}
が得られます。
ｅｎ＝ａn+(1/2)(-2)n
ｆｎ＝ｂn-(1/2)(-2)n
とおくと、ｅ1＝３−１＝２，ｆ1＝１＋１＝２ より、これらを初項とした、公比４の等比数列
ｅｎ＝２・４n-1
ｆｎ＝２・４n-1
以上より、
ａn＝２・４n-1−(1/2)(-2)n＝(1/2){４n−(-2)n}
ｂn＝２・４n-1＋(1/2)(-2)n＝(1/2){４n＋(-2)n}
が得られ、ａn が求める個数です。
答え (1/2){４n−(-2)n}個
算数・数学の部屋に戻る