漸化式と特性方程式に関する考察

疑問
　なぜ、特性方程式で、漸化式が解けるのか？

＜隣接２項漸化式＞
特性方程式
　漸化式　ａ_n+1＝ｂａ_n＋ｃ　に対して、ｘ＝ｂｘ＋ｃ を特性方程式という。
解説
　もとの漸化式が
　　ａ_n+1−α＝ｂ（ａ_n−α）
　の形になれば、ａ_n−α が等比数列になるので、まず、この形にすることを
　目指す。上式のカッコをはずして、
　　ａ_n+1＝ｂａ_n−ｂα＋α
　係数を比較して、
　　ｃ＝−ｂα＋α
　　α＝ｂα＋ｃ
　となり、αは方程式　ｘ＝ｂｘ＋ｃ　の解となる。
　つまり、特性方程式の解を、もとの漸化式の両辺から引くと、等比数列を
　導ける。

＜隣接３項漸化式＞
特性方程式
　漸化式　ａ_n+2＝ｂａ_n+1＋ｃａ_n　に対して、ｘ²＝ｂｘ＋ｃ を特性方程式という。
解説
　もとの漸化式を
　　ａ_n+2−αａ_n+1＝β（ａ_n+1−αａ_n）
　の形にすることを考えます。カッコをはずして、
　　ａ_n+2＝（α＋β）ａ_n+1−αβａ_n
　係数を比較して、
　　ｂ＝α＋β、　ｃ＝−αβ
　よって、２次方程式の解と係数の関係より、α、βは２次方程式
　　ｘ²−ｂｘ−ｃ＝０
　の解となる。逆に、特性方程式の解をα、βとすると、もとの漸化式は
　　ａ_n+2−αａ_n+1＝β（ａ_n+1−αａ_n）
　　ａ_n+2−βａ_n+1＝α（ａ_n+1−βａ_n）
　と書ける。
　初項、第２項をａ₁、ａ₂ とすると、
　　ａ_n+1−αａ_n＝β^n-1（ａ₂−αａ₁）
　　ａ_n+1−βａ_n＝α^n-1（ａ₂−βａ₁）

　（α≠βのとき）
　両辺の差を取って、
　　（β−α）ａ_n＝β^n-1（ａ₂−αａ₁）−α^n-1（ａ₂−βａ₁）
　より、
　　ａ_n＝｛β^n-1（ａ₂−αａ₁）−α^n-1（ａ₂−βａ₁）｝/（β−α）
　（α＝βのとき）
　　ａ_n+1−αａ_n＝α^n-1（ａ₂−αａ₁）
　両辺α^n-1で割って、
　　ａ_n+1/α^n-1−ａ_n/α^n-2＝（ａ₂−αａ₁）
　これは、数列 ａ_n/α^n-2 が等差数列であることを表している。
　初項は　ａ1/α^-1、公差　（ａ₂−αａ₁）であるので、
　　ａ_n/α^n-2＝ａ1/α^-1＋（ｎ−１）（ａ₂−αａ₁）
　両辺 α^n-2 を掛けて、
　　ａ_n＝α^n-1ａ1＋（ｎ−１）（α^n-2ａ₂−α^n-1ａ₁）
　　ａ_n＝（ｎ−１）α^n-2ａ₂−（ｎ−２）α^n-1ａ₁

＜連立漸化式＞
連立漸化式
　ｘn+1＝ａｘ_n＋ｂｙ_n
　ｙn+1＝ｃｘ_n＋ｄｙ_n
は、隣接３項漸化式に帰着できる。

とおくと
　
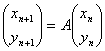
とおけるので、初項 ｘ₁、ｙ₁ に対して、
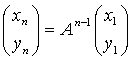　　・・・(1)
となる。
ケーリー・ハミルトンの方程式
　Ａ²−（ａ＋ｄ）Ａ＋（ａｄ−ｂｃ）Ｅ＝Ｏ
に、Ａ^n-1 を掛けて
　Ａⁿ⁺¹−（ａ＋ｄ）Ａⁿ＋（ａｄ−ｂｃ）Ａ^n-1＝Ｏ
よって、
　
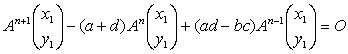
となり、(1) より、
　
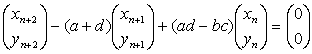
となり、隣接３項漸化式
　ｘ_n+2−（ａ＋ｄ）ｘ_n+1＋（ａｄ−ｂｃ）ｘ_n＝０
　ｙ_n+2−（ａ＋ｄ）ｙ_n+1＋（ａｄ−ｂｃ）ｙ_n＝０
を得る。これより得られる一般項 ｘ_n、ｙ_n はもとの連立漸化式を満たす。


つづく（かも）

「算数・数学」の部屋に戻る