問題
二つの放物線 C: y=x2/2、D: y= -(x-a)2 を考える。a は正の実数である。
(1) C上の点P(t, t2/2)におけるCの接線Lを求めよ。
(2) LがさらにDとも接するとき、LをCとDの共通接線と言う。
2本の(CとDの)共通接線L1とL2を求めよ。
(3) 共通接線L1とL2とCで囲まれた図形の面積を求めよ。
解答
(1)
Cの式をxで微分して、
y’=x
より、点Pにおける接線の傾きは t 。
よって、求める接線は、傾き t で、点(t, t2/2) を通る。その式は、
y=t(x−t)+t2/2
y=tx−t2/2 ・・・答え
(2)
y=tx−t2/2
が、y= -(x-a)2 に接するので、両式を連立させて、
-(x-a)2=tx−t2/2
(x-a)2+tx−t2/2=0
(x-a)2+t(x-a)+at−t2/2=0
x-a に関する方程式と見なしたときの判別式を取って、
t2−4(at−t2/2)=0
3t2-4at=0
これを解いて、t=0,4a/3
よって、求める接線は、
y=0 と y=(4a/3)x−8a2/9
(3)
y=(4a/3)x−8a2/9 と x軸との交点は(2a/3,0)
図の黄色の部分を直接求める方法
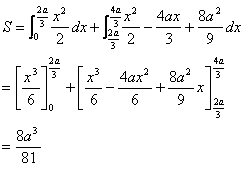
図の黄色と緑を合わせた部分から、緑の部分を引く方法
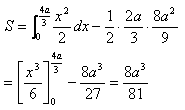
こちらの公式の3を使う方法
(4a/3)3/12=8a3/81
算数・数学の部屋に戻る