問題
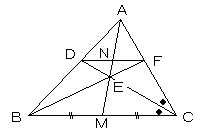
△ABCにおいて、辺BCの中点をMとする。
∠Cの2等分線と辺AB、線分AMとの交点をそれぞれD,E、
直線BEと辺CAとの交点をF、線分AMと線分DFとの交点をNとするとき、次の各問に答えよ。
(1)CF=DF であることを証明せよ。
(2)EM/EN=EC/ED=AB/AD であることを証明せよ。
解答
(1)
メネラウスの定理より
(AE/EM)(MB/BC)(CF/FA)=1
(AE/EM)(MC/CB)(BD/DA)=1
MB=MC より、
CF/FA=BD/DA
よって、△ABCと△ADFは相似となり、DF//BC となるので、
∠DCB=∠CDF(錯角)
条件より
∠DCB=∠DCF
よって、 ∠DCF=∠CDF となり、△CDFは CF=DF の二等辺三角形となる。
以上より、 CF=DF が証明された。
(2)
DF//BC より、△EMCと△ENDは相似(詳しい証明は省略)であるので、
EM/EN=EC/ED ・・・(a)
同様に、△EBCと△EFDが相似なので、
EC/ED=BC/DF ・・・(b)
また、△ABCと△ADFが相似なので、
BC/DF=AB/AD ・・・(c)
(a)(b)(c)より、
EM/EN=EC/ED=AB/AD
となる。
「算数・数学」の部屋に戻る