問題
xy平面上において、x軸上に原点Oと異なる位置にある点Aをとり、点Aを中心とした半径OAの円をかく。
また、この円の外側のx軸上に点B、y軸上に点Cを、線分BCがこの円と異なる2点で交わるようにそれぞれとり、
線分BCと円との交点を、点Bに近い方からP,Qとする。
いま、BP=PQ=QCとなるときOA:ABを最も簡単な整数の比で表すといくらか。
解答
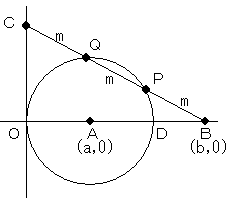
図のように、点A(a,0)、点B(b,0) とし、0<a、2a<<bとします。
また、BP=PQ=QC=m とします。
方べきの定理より、
CQ・CP=CO2
よって、
CO2=m・2m=2m2
CO=√2m
△BCOにおける三平方の定理より
BO2=CB2−CO2=(3m)2−2m2=7m2
よって、
BO=b=√7m
方べきの定理より、
BP・BQ=BD・BO
m・2m=(b−2a)b
2m2=7m2−2√7am
m>0 より、両辺mで割って、整理すると、
2√7a=5m
a=5√7m/14
よって、求める比は
OA:AB=a:(b−a)=(5√7m/14):(9√7m/14)=5:9
算数・数学の部屋に戻る