正２０面体の体積

１辺が１の正２０面体の体積を求めます。

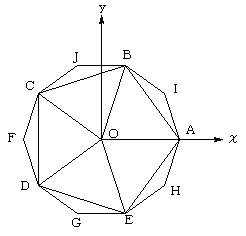
上図は、正２０面体の最も遠い位置にある２点を結ぶ直線方向から、正２０面体を見た図です。
５角形ＡＢＣＤＥは、正５角形ですが、その外接円の中心を、原点Ｏとし、頂点Ａをχ軸上に取ります。
Ａ：（１，０，０）と置きます。（最終的には、ＡＢ＝１ となるように倍率補正します）
このとき、１辺の長さは、
　ＡＢ＝２sin36°
となっています。
問題１２の答えより、この正２０面体のｚ軸方向の長さは、以下のようになります。

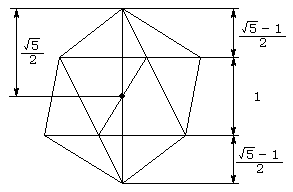
正２０面体の体積は、１つの正三角形と、正２０面体の中心とでできる３角錐の
２０倍ですから、まず１つの３角錐の体積を求めます。
この三角錐は、底面が１辺 ２sin36°の正三角形、側面は合同な二等辺三角形で、
等辺の長さが、√５／２となります。
正三角形の１つの頂点をＡ、重心をＭ、正２０面体の中心をＮとすると、
下図のような直角三角形が出来ます。このとき、ＭＮが三角錐の高さとなります。

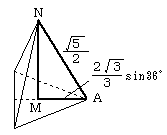
これより高さＭＮを求めると、ＭＮ＝√（（５＋２√５）／１２）
三角錐の底面積は
　1/2×(２sin36°)²sin60°＝（５√３−√１５）／８
よって、三角錐の体積は、
　1/3×（５√３−√１５）／８×√（（５＋２√５）／１２）
　＝（５√３−√１５）／２４×√（（５＋２√５）／１２）
また、正２０面体の体積は、この２０倍で、
　５（５√３−√１５）／６×√（（５＋２√５）／１２）
ただしこれは、１辺が、ＡＢ＝２sin36°の場合なので、１辺が１に換算するため、
８sin³36°で割って、整理すると、以下の体積を得ます。

体積＝

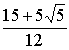
「算数・数学」の部屋に戻る