問題１２の解答

この問題では、底面の半径はすでに１とわかっているので、高さを求める問題と考えることにします。

図のように、上面の五角形の頂点Ａから、底面に垂線をおろし、その足をＣとします。
また、点Ｂは下面の五角形の頂点のうち、Ｃにもっとも近い点です。

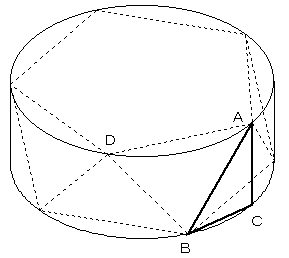
ここで、△ＡＢＣは∠ＡＣＢ＝９０°の直角三角形で、ＡＣが求める高さになります。

△ＡＢＤは正三角形なので、ＡＢ＝ＡＤとなり、ＡＢは、正五角形の１辺と同じ長さです。
その長さは、ＡＢ＝２ｓｉｎ３６°

ＢＣは、底面の円に内接する正１０角形の１辺に相当しますから、
その長さは、ＢＣ＝２ｓｉｎ１８°
、
より、
ＡＣ²＝ＡＢ²−ＢＣ²＝４ｓｉｎ²３６°−４ｓｉｎ²１８°
　　
ＡＣ＞０　より、　ＡＣ＝１　となります。
よって、求める体積は
１×１×π×１＝π　・・・・答え

解答を寄せて下さった皆さん。ありがとうございました。

問題に戻る

「算数・数学の部屋」に戻る