問題
xy-平面上に不等式
logxy+2logyx<3
を満たす点(x,y)の存在する範囲を図示せよ。
解答
公式 logab=logb/loga より、
logyx=1/logxy
よって、X=logxy とおくと、与式は
X+2/X<3
と書ける。(y は底にもなっているので y≠1 より、X≠0)
X>0 のとき、
X2+2<3X
X2-3X+2<0
(X-1)(X-2)<0
より、
1<X<2 …………(1)
これは、X>0 を満たす。
X<0 のとき
X2+2>3X
(X-1)(X-2)><0
より、
X<1 または X>2
X<0 を考慮して、
X<0 …………(2)
(1) より、
1<logxy<2
1<logy/logx<2
※底は1以外の任意の正の数ですが、ここでは特に1より大きい数とします。
底を1未満の正の数としても、途中が変わるだけで、結果は同じです。
logx<0 のとき、つまり、0<x<1 のとき、
logx>logy>2logx=logx2
底を1より大きいとしたので、
x>y>x2 …………(a)
logx>0 のとき、つまり、1<x のとき
logx<logy<2logx=logx2
より、
x<y<x2 …………(b)
(2) より、
logxy<0
logy/logx<0
logx<0 のとき、つまり、0<x<1 のとき、
logy>0
よって、y>1 …………(c)
logx>0 のとき、つまり、1<x のとき
logy<0
よって、y<1 …………(d)
以上の結果をグラフに描くと以下のようになります。
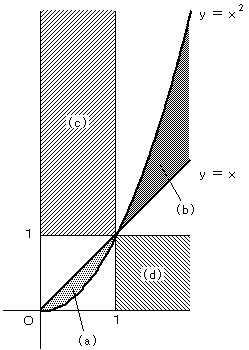
ただし、境界線上の点は含みません。
算数・数学の部屋に戻る