問題
mを実数とする。Oを原点とする座標平面上で、放物線y=x2 とその曲線上にある2点
A(a,ma+1)、B(b,mb+1) (a<0<b)
を考える。
(1) 2点A,Bのx座標a,bは、mを用いて
a=(m−√D)/[A]、 b=(m+√D)/[B]
と表される。ここで、Dの式は
D=m2+[C]
である。
(2) 線分ABとy軸の交点の座標を(0,c)とおくと、c=[D]である。
(3) さらに、3点O,A,Bを頂点とする三角形OABの面積Sをa,bを用いて表すと、
S=(1/2)[E]
である。
ただし、[E]には、次の(0)〜(5)の中から適切なものを選びなさい。
(0)a+b (1)a-b (2)b-a (3)a2+b2 (4)a2-b2 (5)b2-a2
また、mを用いてSを表すと
S=([F]/[G])√(m2+[H])
であるから、Sが最小となるのは、m=[I]のときであり、その最小値は S=[J]である。
解答
(1)
A,Bの座標はA(a,a2)、B(b,b2)でもあるので、
a2=ma+1、b2=mb+1
これらをa<0<b の条件下で解いて、
a=(m−√(m2+4))/2, b=(m+√(m2+4))/2 ・・・(i)
[A]=[B]=2、[C]=4
(2)
A,Bともに、y=mx+1 上の点であるので、y軸との交点はこの直線のy切片となり、
c=1 ・・・ [D]
(3)
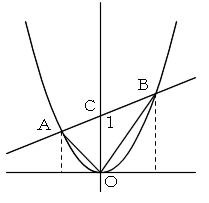
C(0,1) とします。
S=△ACO+△BCO
△ACO=(-1/2)a
△BCO=(1/2)b
より
S=(1/2)(b−a) ・・・答えは [E]=(2)
これに、(i) を代入すると、
S=(1/2)√(m2+4)
[F]=1、[G]=2、[H]=4
Sの最小値はm=0のとき1。
[I]=0,[J]=1
算数・数学の部屋に戻る