問題1
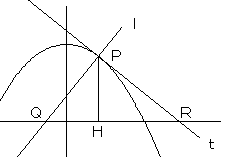
Oを原点とする座標平面上に放物線C1:y=−x2/4+x/4+3と直線 l :3x+4y-12=0がある。
C1と l は2点A(0,3) B(4,0)で交わる。
3点A,B,Oを通る円C2の中心の座標は(2、3/2)、半径は5/2である。
l と C1 によって囲まれた部分(境界を含む)をD、
C2の周および内部が l によって分割される二つの部分のうち、Oを含む部分(境界を含む)をEとする。
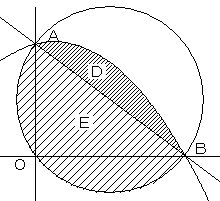
(1)DまたはEを点(x、y)が動くとき、3x+4yは
x=□、y=□
のとき最大値□をとる。また、最小値は□である。
(2)点Pが領域Dを、点Qが領域EをA,B,P,Qが四角形の頂点となるように動くとき、
四角形APBQの面積の最大値は□である。
解答1
(1)
直線m:3x+4y=k
とおきます。k がいろいろ変わるとき、直線m のグラフは l に平行な状態で
上下に動きます。このとき、y切片は k/4
直線mが領域DまたはEと共有部分を持ちながら変化するとき、y切片が
最大(最小)のとき k が最大(最小)になります。
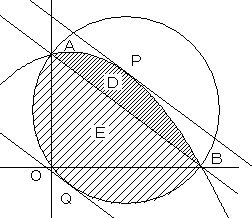
図において、直線mが点Pを通るとき k が最大、点Qを通るとき k が最小になります。
<Pを求める>
y=−x2/4+x/4+3
の接線で、傾きが−3/4 のものを見つけます。
yをxで微分して、
y’=−x/2+1/4
y’=−3/4 より、x=2
このとき y=5/2
よって、Pの座標 (2,5/2)
このとき
3x+4y=16・・・最大値
<Qを求める>
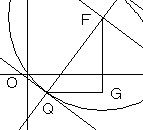
C2 の中心をFとし、図のように直角三角形FGQを作ると、
FQ=5/2、FG:GQ=4:3 より
FG=2,GQ=3/2
よって、Qのx座標:2−3/2=1/2、Qのy座標:3/2−2=-1/2
このとき、
3x+4y=-1/2・・・最小値
(2)
△ABPと△ABQに分けて、それぞれが最大となることを考えます。
ABを底辺として、出来るだけABから遠い位置にP、Qを置けば、面積最大となりますが、
それらは、上の図のP、Qにあたります。
△ABQのABを底辺としたときの高さは FQ=5/2 とわかっていますので、ここでは、
△ABPの高さを求めます。
(解き方1)
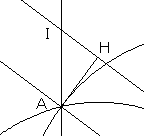
点Pを通り l に平行な直線を n とし、点Aから直線 n に垂線AHをおろします。
また、直線 n のy切片をI:(0,4)とします。
AI=1,AH:HI:IA=4:3:5 より、AH=4/5・・・高さ
(解き方2)
点P: (2,5/2) から 直線 l :3x+4y-12=0 までの距離は、公式より
|3・2+4・(5/2)−12|/√(32+42)=4/5・・・高さ
また、AB=√(32+42)=5
以上より、
△ABP=5×4/5÷2=2
△ABQ=5×5/2÷2=25/4
四角形APBQの面積=2+25/4=33/4
問題2
放物線 C:y=-x2+1 (x>0) の上の点P(x、y)における接線をt、
それに直交しPを通る直線を l とする。
(1) l と x軸との交点のx座標が最小となるときの点Pの座標を求めよ。
答 P(√6/6、5/6)
(2) このとき、t と l と x軸とで囲まれた図形の面積を求めよ。
答 125√6/432
解答2
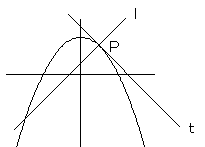
(1)
y’=-2x
より、tの傾きは -2x。
x>0 より l の傾きは 1/2x。
点Pの座標を(a,-a2+1) とおくと、点Pにおける l の傾きは 1/2a。
l の式は
y=(x-a)/2a-a2+1
この直線とx軸との交点のx座標は、y=0 とおいて
x=2a3-a
x を a で微分すると、
dx/da = 6a2-1
dx/da=0 となるのは a=±√6/6
増減表を書くと