問題(太字はベクトルを表します)
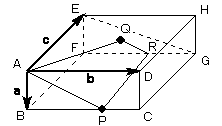
AB=1 AD=3 AE=2 の直方体 ABCD-EFGH があり
AB=a、AD=b、AE=c
とする。
辺BCを2:1に内分する点をPとし、三角形EFGの重心をQとする。
3点A,P,Qを通る平面と辺FGの交点をRとするとき、FR:RG を求めよ。
解答1(ベクトルを使った方法)
AP=a+2b/3
AQ=2a/3+b/3+c
と表せます。
RはAPQと同じ平面上にあるので、
AR=sAP+tAQ (s、t は実数) ・・・(1)
と表せます。
一方、FR=ub とすると、
AR=AB+BF+FR
=a+ub+c ・・・(2)
と表せます。
(1) より、
AR=(s+2t/3)a+(2s/3+t/3)b+tc
これを (2) と比較して、
s+2t/3=1
2s/3+t/3=u
t=1
これを解いて、
t=1
s=1−2/3=1/3
u=2/9+1/3=5/9
以上より、
FR=FG×(5/9)
となるので、 FR:RG=5:4 となります。
解答2(図形として解く方法)
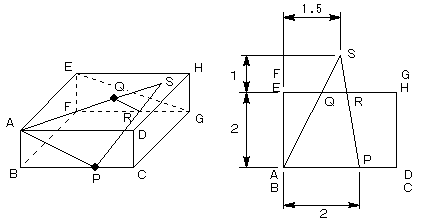
AQの延長線が、長方形BCGFを含む平面と交わる点をSとします。
直線PSは、APQを通る平面と、長方形BCGFを含む平面との交線なので、
FGとPSの交点がRとなります。
AからQ、さらにSに線を延ばしたとき、Qまで来た時点で、直方体の高さの
2/3 を下りています。残りの1/3 を下りるためには、AQの半分だけ延ばせばいいので、
QS=AQ/2
となります。
この様子を、真上から見ると、図の右のようになりますが、この図でFQはFGの1/3の位置にあるので、
FQ=1 (ただし、平面図上での長さ)
より、Sの位置はFから 1.5 右に行った位置になります。
右の図よりFRの長さを求めると、
FR=1.5+0.5/3=5/3
一方、
RG=3−5/3=4/5
よって、 FR:RG=5:4 となります。
算数・数学の部屋に戻る