問題
関数f(x)=x2-4|x|+kの最小値をm(k),最大値をM(k)とする。
(1) m(k)=2のとき、定数kの値を求めよ。
(2) -1≦x≦5のとき、m(k),M(k)をkで表せ。
(3) f(x)=0の解が4個になるようなkの値の範囲を求めよ。
(4) 関数y=f(x)のグラフを直線y=kに関して対称移動するとき、その関数の最大値を求めよ。
解答
y=x2-4|x|+k のグラフは、以下のようになります。
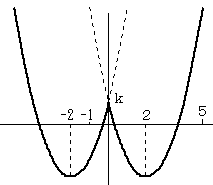
(1)
グラフより、x=−2 または x=2 で f(x) は最小となり、その値は、
f(-2)=f(2)=k-4
より、m(k)=k-4。
k-4=2 より、 k=6
(2)
グラフより、
m(k)=f(2)=k-4
M(K)=f(5)=k+5
(3)
y=f(x) のグラフは、k の値に従って、上下(y軸方向)に動きます。
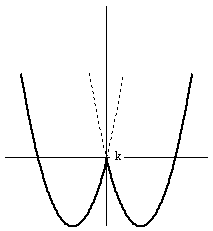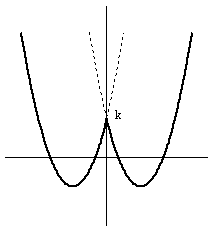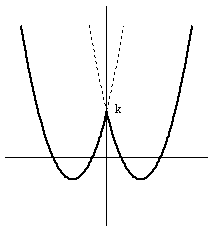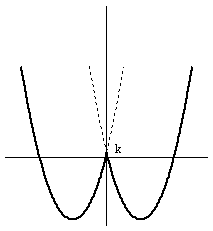
このグラフが、x軸と4点で交わるkの範囲はグラフより、
0<k<4
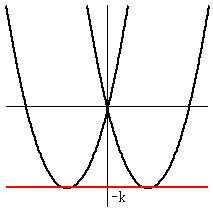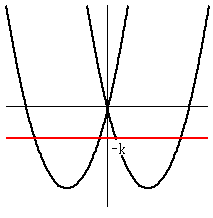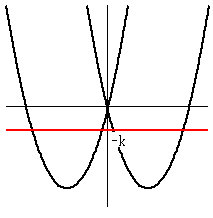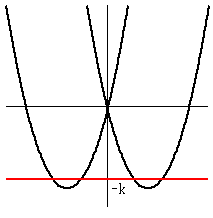
y=x2-4|x| のグラフを固定しておいて、そこに y=-k のグラフを交叉させても同様です。
ただし、この場合、y=-k なので、符号に注意。
(4)
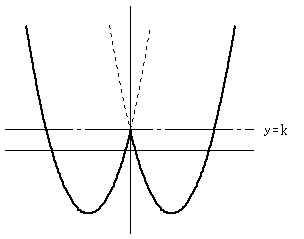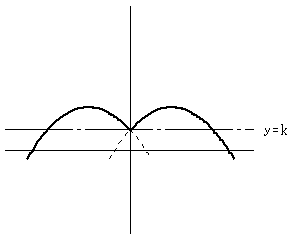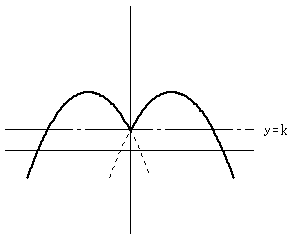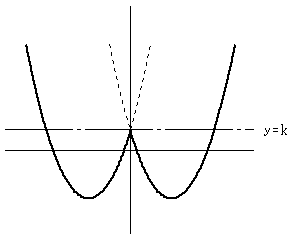
y=f(x) のグラフを、y=k に対称に移動すると、元の最小値が最大値となるので、
元のグラフの最小値 k-4 だから
2k-(k-4)=k+4
算数・数学の部屋に戻る