問題1
xについての2次方程式x2-2a|x|+9=0が、-5と5の間に相異なる4つの実数解をもつためのaの値の範囲を求めよ。
解答1
左辺は
x>0 のとき x2-2ax+9
x<0 のとき x2+2ax+9
x=0 のとき 9
と書けます。
y=x2-2a|x|+9
のグラフは、a の正負によって、次の2通りになります。a=0 の場合は省略。
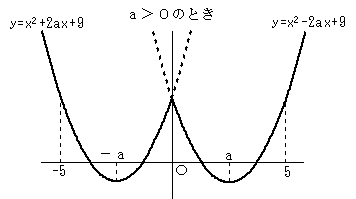
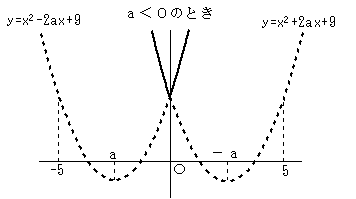
このうち、4つの解を持つ可能性のあるのは、a>0のときです。
グラフの対称性より、y=x2-2ax+9 のグラフが0<x<5の範囲に2つの実数解を持てばいいことがわかります。
f(x)=x2-2ax+9 とおきます。
y=f(x) のグラフの軸は、x=a です。
0<x<5の範囲に2つの実数解を持つ条件は、
・判別式:a2-9>0 より、a<-3 または a>3
・軸が0と5の間にある: 0<a<5
・f(0)=9>0
・f(5)=34-10a>0 より a<3.4
以上より、aの範囲は 3<a<3.4
問題2
xについての方程式ax2+(3a-8)x+4(a-6)=0が少なくとも1つの正の解をもつように、定数aの値の範囲を定めよ。
解答2
f(x)=ax2+(3a-8)x+4(a-6) とおきます。
xについての「2次」方程式、とは書いていないので、a=0 の可能性も考慮します。
(1) a=0 のとき
-8x-24=0 より、x=-3 となり、不適
(2) a≠0 のとき
判別式:(3a-8)2-16a(a-6)=-7a2+48+64>0
より、-8/7<a<8 ・・・(i)
2解が正と負のとき
解と係数の関係より
4(a-6)/a<0
これを解いて、0<a<6 ・・・(ii)
2解がともに正であるとき
軸:-(3a-8)/2a>0
これを解いて、0<a<8/3 ・・・(iii)
f(0)=4(a-6)>0 より、a>6 ・・・(iv)
(i) かつ (ii) または {(iii) かつ (iv)} より、
0<a<6
問題3
aを実数の定数とする。関数f(x)=x2-ax+a+2が a≦x≦a+1 の範囲で、常に不等式f(x) > 0を満たすようなaの値の範囲を求めよ。
解答3
・a=0 のときは、f(x)=x2+2>0 より、条件を満たします。
・a>0のとき
y=f(x) のグラフは、以下のようになります。
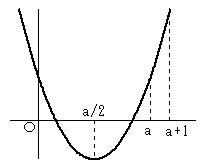
f(a)<f(a+1) は明らかなので、
f(a)>0 をいえばよい。
f(a)=a+2>0 より、a>-2
よって、 a>0 のときは、すべて条件を満たします。
・a<0 のとき
y=f(x) のグラフは、以下のようになります。
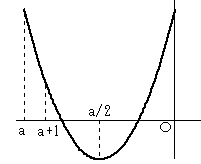
*a/2≦a+1 のとき、つまり、-2≦a<0 のとき
範囲内に頂点を含むので、グラフ全体が正でなければならない。
判別式:a2-4(a+2)=a2-4a-8<0
これを解いて、 2−2√3<a<2+2√3
よって、 2−2√3<a<0
*a+1<a/2 のとき、つまり a<-2 のとき
f(a+1)>0 をいえばよい。
f(a+1)=2a+3>0 より、 a>-3/2
よって、条件を満たすaの範囲はない。
以上より、2−2√3<a
算数・数学の部屋に戻る