問題
次の条件を満たす四角形O-ABCDを考える
四角形ABCDは一辺の長さが1の正方形である
OA=OB=OC=OD=2
線分OB上の点Eを、線分の長さの和AE+ECが最小になるように取る。三点A,C,Eを通る平面と直線ODとの交点をFとする。
OFの長さと四角錘O-AECFの体積を求めよ
解答
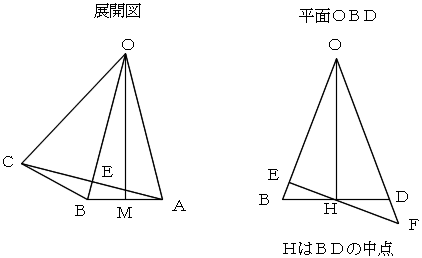
上図の左は、この四角錐の展開図の一部です。
A−E−Cが直線になったときにAE+ECは最小になります。
対称性より、∠AEO=90° となります。
△OABにおいて、ABの中点をMとすると、三平方の定理より
OM=√(OB2−MB2)=√15/2
よって、△OABの面積はABを底辺とすると、OMが高さとなり、
△OAB=(1/2)×1×√15/2=√15/4
一方、OBを底辺とすると、AEが高さとなるので、
AE=√15/4÷2×2=√15/4
△OAEにおける三平方の定理より
OE=√(OA2−AE2)=7/4
よって、BE=1/4 となります。
上図の左は、3点O,B,Dを通る平面に、垂直な方向から見た四角錐です。
この図上では、3点A,C,Eを通る平面は直線EFで表されています。
点HはBDの中点(ACの中点でもある)ですが、この図では、AもCも、Hと同じ位置にあります。
EHの延長線と、ODの延長線が交わる点がFとなります。
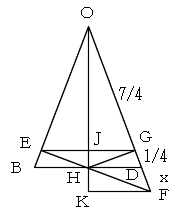
OD上において、OG=7/4 となる点をGとし、また、DF=xとします。
また、EGの中点をJ、FからOHにおろした垂線の足をKとします。
△OJGと△OKF の相似より
JG:KF=(7/4):(2+x)
△JGHと△KFHの相似より、
JG:KF=(1/4):x
よって、(7/4):(2+x)=(1/4):x
これを解いて、x=1/3
よって、OF=2+1/3=7/3 ・・・答え1
四角錘O-AECFは、四角錐O-ABCD から三角錐E-ABCを引いて、三角錐F-ADC を加えた立体です。
四角錐O-ABCD の体積Vは (1/3)×1×OH
ここで、△OBHにおける三平方の定理より
OH=√(OB2−BH2)=√(7/2)
よって、V=√14/6
Vに対して、三角錐E-ABC は、底面積 1/2 高さ 1/8 なので、体積はV/16
三角錐F-ADC は、底面積 1/2 高さ1/6 なので、体積は V/12
よって、四角錘O-AECF の体積は V(1−1/16+1/12)=(49/48)V=49√14/288 ・・・ 答え2
算数・数学の部屋に戻る