問題
半径rの球面上に異なる4点A,B,C,Dがある。
AB=CD=√2、AC=AD=BC=BD=√5であるときrを求めよ。
解答
四面体ABCDは4面が合同な三角形で出来ています。
ABの中点をM、CDの中点をNとしたとき、MNの中点が球の中心になります。
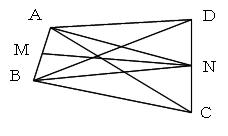
△BNDにおいて、
BN=√(BD2−DN2)=3/√2
同様にAN=3/√2
△AMNにおいて、
MN=√(AN2−AM2)=2
よって、MNの中点をOとすると、点Oが球の中心となり、
MO=MN/2=1
△AMOにおいて
OA=√(AM2+MO2)=√(3/2)=√6/2 ・・・ 答え
算数・数学の部屋に戻る