うっしーさんからの質問１

問題
x²−2xy＋2y²＝1　のグラフはどんな形か？

解答
この式のグラフは、ある２次曲線を原点周りに回転させたと考えます。
ある点（ｘ、ｙ）を、原点周りにθ回転させた点(X,Y)は、
　Ｘ＝ｘcosθ−ｙsinθ
　Ｙ＝ｘsinθ＋ｙcosθ
と表せます。（Ｘ，Ｙ） を、 x²−2xy＋2y²＝1 に代入して、
　(ｘcosθ−ｙsinθ)²−2(ｘcosθ−ｙsinθ)(ｘsinθ＋ｙcosθ)+2(ｘsinθ＋ｙcosθ)²＝１
これを展開して整理すると、
　ｘ²(cos²θ−2cosθsinθ＋2sin²θ)＋ｙ²(sin²θ＋2cosθsinθ＋2cos²θ)
　　＋2ｘｙ(sin²θ−cos²θ＋cosθsinθ)＝１　・・・(1)
ｘｙの項の係数に注目して
　2(sin²θ−cos²θ＋cosθsinθ)＝sin2θ−2cos2θ
　　＝√5(cosαsin2θ−sinαcos2θ)
　　＝√5sin(2θ−α)
　ただしαは、cosα＝1/√5、sinα＝2/√5 となる角。
ｘｙの係数が０になるように考えると、
　sin(2θ−α)＝０
つまり、例えば、θ＝α/2 なる角θを考えると、

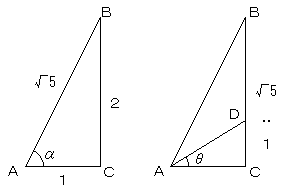
図において、ＡＣ＝１ とすると、ＤＣ＝２/(√5＋１)
よって、ＡＣ：ＤＣ＝(√5＋１)：２
ＡＤ＝√(10＋2√5)
より、sinθ＝２/√(10＋2√5)、cosθ＝(√5＋１)/√(10＋2√5)
また、sin²θ＝(5−√5)/10、cos²θ＝(5＋√5)/10、sin2θ＝sinα＝2√5/5
などを利用して、(1) の係数を求めると、
　cos²θ−2cosθsinθ＋2sin²θ＝１＋sin²θ−sin2θ
　　＝１＋(5−√5)/10−2√5/5＝(3−√5)/2
　sin²θ＋2cosθsinθ＋2cos²θ＝１＋cos²θ＋sin2θ
　　＝１＋(5＋√5)/10＋2√5/5＝(3＋√5)/2
よって、求める図形は、楕円
　(3−√5)ｘ²/2＋(3＋√5)ｙ²/2＝１
をθだけ回転させた図形。

算数・数学の部屋に戻る