問題
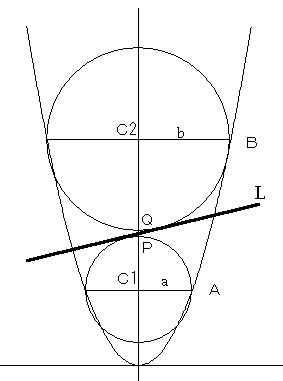
図のように、放物線y=x2 と、y軸上の点C1 を中心、半径a の円C1 と、y軸上の点C2 を中心、半径b の円C2 があります。
点A、Bは円C1、C2と放物線y=x^2との交点(ただしx座標が正)であり、C1A、C2Bはx軸に平行である。
また、点P、Qはそれぞれ円C1、C2とy軸との交点のうち、C1 とC2 の間にある点である。
PQ=6として次の問いに答えなさい。ただし、a、bは自然数とし、a<bとする。
(1)a、bの値を求めなさい。
(2)円C1、C2の共通内接線Lの方程式を求めなさい。
解答
(1)
2つの半径、a,bに対して、C1,C2 のy座標は、a2、b2 であるので、
Pのy座標は、a2+a
Qのy座標は、b2−b
これの距離が6なので、
(b2−b)−(a2+a)=6
展開して、
b2−a2−a−b=6
(b−a−1)(b+a)=6
a,b は自然数なので、b−a−1、b+a ともに自然数であり、
b−a−1<b+a も明らかなので、
b−a−1=1 かつ a+b=6 ・・・(i)
b−a−1=2 かつ a+b=3 ・・・(ii)
のいずれかです。このうち、自然数の解になるのは、(i) から得られる
a=2,b=4 です。
(2)
<図形による方法>
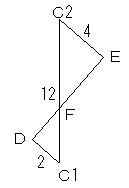
点C1、C2 から、Lにおろした垂線の足を、D,E とし、Lとy軸の交点をFとします。
C1D=2、C2E=4、C1C2=12
であり、△C1DFと△C2EF が相似であることより、
C1F:C2F=1:2
となり、C1F=4,C2F=8 より、Fのy座標は、4+4=8
また、△C1DF、△C2EF は、1:2:√3 の三角形であり、Lの傾きは√3 であることがわかります。
よって、Lの式は、
y=(√3)x+8
また、対称性から、
y=−(√3)x+8
も、解となります。
算数・数学の部屋に戻る