問題(出典はこちら)
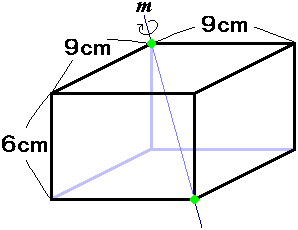
縦、横、高さがそれぞれ9cm、9cm、6cmである直方体Vがあります。
この直方体の対角線の1本をmとして、直線mを軸としてVを180度回転させてできる直方体をWとします。
さて、VとWの共通部分の立体の体積は何cm3でしょうか。
解答
図のように、対角線の中点を通り、対角線に垂直な平面で、切断することを考えます。
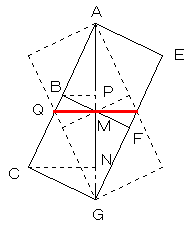
図において、ABCD(DはBと重なっている)が、9×9の正方形で、AE,BF,CGなどが、6cmの辺です。
対角線AGの中点をM。C、Bから、AGに下ろした垂線の足を、N、Pとします。
△ACG,△ANC,△CNG は相似な直角三角形なので、
AC/CG=AN/NC=NC/NG
より、
(AN/NC)(NC/NG)=(AC/CG)(AC/CG)
AN/NG=AC2/CG2
の関係があります。
AC2=2×□ABCD=9×9×2=162
CG2=6×6=36
より、
AN:NG=162:36=9:2=18:4
PはANの中点なので、
AP:PN:NG=9:9:4
MはAGの中点なので、
AP:PM:MN:NG=9:2:7:4
以上より、BQ:QC=PM:MN=2:7 となり、BQ=2cm、QC=7cm となります。
また、Mは、BFの中点でもあり、BM=MF=3cm です。
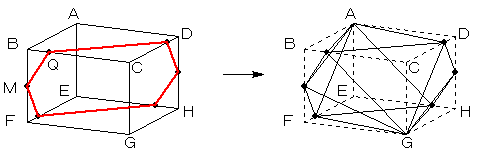
よって、求める立体は、図のように、
9×9×6=486(cm<SUP>3</SUP>)
の直方体から、直角をはさむ3辺が、
7×7×6 の三角すい(C,Eを含むもの:体積49)を2つ
3×2×9の三角すい(B,D,F,Hを含むもの:体積9)を4つ
を取り去ったもので、体積は、
486−49×2−9×4=352(cm3)
算数・数学の部屋に戻る