問題
(1) f(x)=x3+2x2+1の極大値と極小値が、g(x)=x3+3px+qの極大値と極小値に、それぞれ等しい。
実数p,qの値を求めよ。
(2) f(x)=x3-2x2,g(x)=-x2+x+aとする。
x≧-1のどのようなx1,x2にたいしてもf(x1)≧g(x2)となる実数の定数aの値の範囲を求めよ。
解答
(1)
f'(x)=3x2+4x より、f'(x)=0 となるのは、x=0, -4/3 のときで
f(0)=1 ・・・ 極小値
f(-4/3)=59/27 ・・・ 極大値
一方、g'(x)=3x2+3p より、 g'(x)=0 となるのは、x=±√(-p) のとき。ただしp≦0。
g(√(-p))=2p√(-p)+q=1
g(-√(-p))=-2p√(-p)+q=59/27
これを解いて、p=-4/9,q=43/27
(2) 言いかえると、x≧-1 における f(x) の最小値が、g(x) の最大値以上であるということです。
y=f(x), y=g(x) のグラフを描くと以下のようになります。
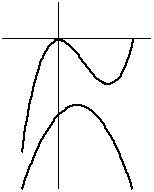
f'(x)=3x2-4x より、極大値は f(0)=0, 極小値はf(4/3)=-32/27
一方 f(-1)= -3<-32/27 より、x≧-1 における f(x) の最小値は -3。
g(x) の最大値は g(1/2)=a+1/4 より、
-3≧a+1/4
a≦-13/4
算数・数学の部屋に戻る