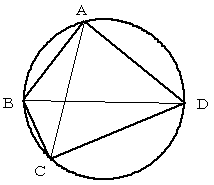
円に内接する四角形ＡＢＣＤがあるとき、以下の等式が成り立つ。
　　ＡＢ・ＣＤ＋ＢＣ・ＤＡ＝ＡＣ・ＢＤ

＜証明＞

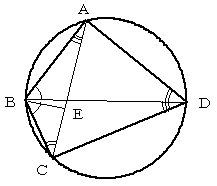
ＡＣ上に
　∠ＣＢＥ＝∠ＡＢＤ
となるような点Ｅをとる。このとき、
　△ＢＥＡ∽△ＢＣＤ　より、
　　ＡＥ・ＢＤ＝ＡＢ・ＣＤ・・・(1)
　△ＢＥＣ∽△ＢＡＤ　より、
　　ＣＥ・ＢＤ＝ＢＣ・ＤＡ・・・(2)
(1)+(2) より、
　（ＣＥ＋ＡＥ）ＢＤ＝ＡＢ・ＣＤ＋ＢＣ・ＤＡ
　ＡＣ・ＢＤ＝ＡＢ・ＣＤ＋ＢＣ・ＤＡ
証明終

「算数・数学の部屋」に戻る