1つの直線上に3点A,B,Cがあり、別の直線上に3点P,Q,Rがあり、
AQとBPの交点X、BRとCQの交点Y、CPとARの交点Zが存在するならば、
3点X,Y,Zは一直線上にある。
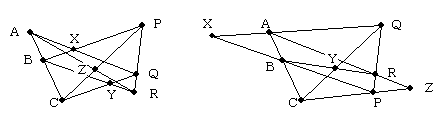
証明
パップスの定理(3)
1つの直線上に3点A,B,Cがあり、別の直線上に3点P,Q,Rがあり、
AQとBPの交点X、BRとCQの交点Y、CPとARの交点Zが存在するならば、
3点X,Y,Zは一直線上にある。

証明
| △XAPと△XARは底辺XAを共有しているので △XAP/△XAR=PQ/QR 同様に△YCPと△YCRは底辺YCを共有していることより △YCP/△YCR=PQ/QR 従って △XAP/△XAR=△YCP/△YCR ………(1) |
  |
| 同様にして△XAPと△XCPは底辺XPを共有、 △YARと△YCRは底辺YRを共有していることから △XAP/△XCP=△YAR/△YCR(=AB/BC) ………(2) (1)÷(2)より △XCP/△XAR=△YCP/△YAR すなわち △XCP/△YCP=△XAR/△YAR ………(3) |
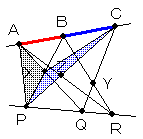  |
| ここで、△XCPと△YCPは底辺CPを共有しているので、CPとXYの交点をSとすれば △XCP/△YCP=XS/SY ………(4) 同様に△XARと△YARは底辺ARを共有しているので、ARとXYの交点をTとすると △XAR/△YAR=XT/TY ………(5) (3),(4),(5)より XS/SY=XT/TY 従ってS,TはXYの間にあるので同一点であり、Zとも一致する。 すなわちX,Y,Zの3点は一直線上にある。 |
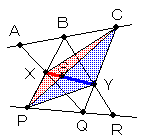 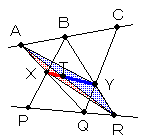 |