問題
n×nのマス目の正方形ABCDにおいて,対角線ACに交わる長方形の個数を求めよ。
解答1
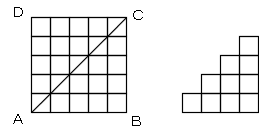
図は、5×5の場合ですが、5×5の図形全体で作れる長方形から、右の階段状の図形だけで出来る
長方形を(2倍して)引くことを考えます。
まず、n×nの正方形から、切り取れる長方形は、
縦線の選び方は n+1C2、横線も同様で、合計 n2(n+1)2/4 個。
このとき、n−1段の階段状の図形が出来ます。
n段の階段状の図形から切り取れる長方形の数を S(n) とします。
まず、S(1)=1 です。
次に、下に1×2の長方形を付け加えると、元々ある1個の長方形を、下に1マス伸ばして出来る長方形が1個。
付け加えた1×2の長方形だけで出来るのが、3C2=3(個)。計4個増えて、S(2)=5 となります。
次に、下に1×3の長方形を加えると、2段の時に、新しく増えた4個の長方形を下に1マス伸ばして出来る長方形が4個。
付け加えた1×3の長方形だけで出来るのが、4C2=6(個)。計10個増えて、S(3)=15 となります。
これを、一般化すると、n+1段の階段状の図形の下に、1×(n+2)の長方形を付け加えると、
n+1段の時に新しく増えた、S(n+1)−S(n) 個の長方形を下に1マス伸ばして出来る長方形がS(n+1)−S(n) 個。
付け加えた1×(n+2)の長方形だけで出来るのが、(n+3)C2=(n+3)(n+2)/2 個。よって、
S(n+2)=S(n+1)+{S(n+1)−S(n)}+(n+3)(n+2)/2=2S(n+1)−S(n)+(n+3)(n+2)/2
という漸化式が出来ます。変形して、
S(n+2)−S(n+1)=S(n+1)−S(n)+(n+3)(n+2)/2
T(n)=S(n+1)−S(n) とおくと、T(1)=4 であり、
T(n+1)=T(n)+(n+3)(n+2)/2
T(n+1)−T(n)=(n2+5n+6)/2
階差数列の公式より、
T(n)=(n3+6n2+11n+6)/6
S(n)=n(n+1)(n+2)(n+3)/24
が得られます。
よって、求める個数は、
n2(n+1)2/4−S(n-1)×2=n2(n+1)2/4−(n-1)n(n+1)(n+2)/12=n(n+1)(n2+n+1)/6
追記
チャオさんより、S(n) の求め方について、ご指摘いただきましたので、載せておきます。
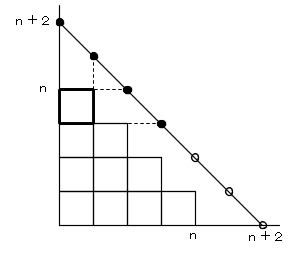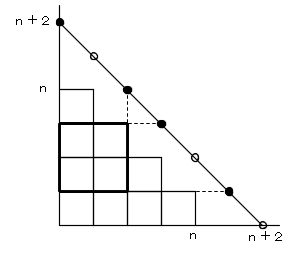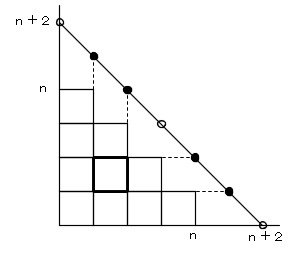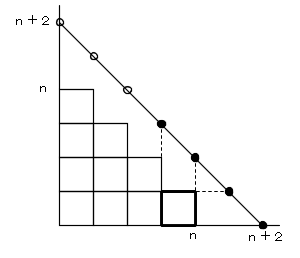
図のように、座標平面上に、n段の階段状の図形を置き、(n+2,0) と (0,n+2) とを結んだ線分上の
n+3個の格子点を考えると、これら n+3 個の格子点から、4個の点を選ぶことと、n段の階段状の図形上に
作られる長方形とが対応します。
(4点のうち、y座標の大きい2つを横幅、x座標の大きい2つを縦幅(高さ)に対応させます)
よって、求める長方形の数は、
n+3C4=n(n+1)(n+2)(n+3)/24
となります。
「算数・数学の部屋」に戻る