ＴＡＮＥさんからの質問９

（）はベクトルを表すものとします。

問題１
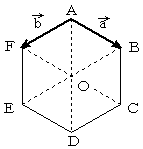
正六角形ＡＢＣＤＥＦにおいて、(ａ)＝(AB)、 (ｂ)＝(AF)とする。
次の２点を通る直線上の点Pの 点Aに関する位置ベクトルを(ｐ)とするとき、
(ｐ)が 満たすベクトル方程式を媒介変数 ｔ を用いて表せ。
（１）B、E　　（２）A、D　　（３）C、E


解答１
一般に２点Ａ(a)、Ｂ(b) を通る、直線の方程式は、
　(p)=(1-t)(a)+t(b)
と書けます。
ＡＢを t:1-t に分ける点の位置ベクトルを ｔ を使って表した式です。


（１）
解法１
　(AE)=(a)+2(b)
なので、(p) の式は、
　(p)=(1-t)(a)+t{(a)+2(b)}
　　=(a)+2t(b)
2t は任意の実数を取るので、 t と置き直して、
　(p)=(a)+t(b)

解法２
　ＢＥの式を求める代わりに、ＢＯの式を求めても同じである。
　(AO)=(a)+(b)
なので、(p) の式は、
　(p)=(1-t)(a)+t{(a)+(b)}
　　=(a)+t(b)

図形的に考えると、(a) の位置（Ｂ）から、(b) の方向に、任意の長さ移動した点の集まり
ですので、ＢＥを表すことになります。

（２）
　(AD)=2(a)+2(b)
　(AA)=(0)
なので、(p) の式は、
　(p)=(1-t)(0)+t{2(a)+2(b)}
　　=2t(a)+2t(b)
2t を t に置き直して、
　(p)=t(a)+t(b)

（３）
　(AC)=2(a)+(b)
　(AE)=(a)+2(b)
なので、(p) の式は、
　(p)=(1-t){2(a)+(b)}+t{(a)+2(b)}
　　=(2-t)(a)+(1+t)(b)
このままでも良いですが、1+t を t に置き直して、
　(p)=(3-t)(a)+(b)
また、
　(p)=3(a)+t{(b)-(a)}
とすると、図形的な意味が読みとれます。

問題２
定点Ｏに関する３点A、B、Pの位置ベクトルを、 それぞれ(ａ)、(ｂ)、(ｐ)とする。
点Pが次の図形上に あるとき、(ｐ) の満たすベクトル方程式を求めよ。
（１）点Ｏを中心とし、半径OAの円周
（２）点Aを中心とし、半径OAの円周
（３）点Bを中心とし、半径ABの円周
（４）線分ABを直径とする円周

解答２
円のベクトル方程式は主に、「半径＝一定値」「直径の円周角＝９０°」の
どちらかの形になります。

	（１）ＯＰの長さがＯＡと常に等しいので、 　|(p)|=|(a)| または、左図のＡＰとＡ’Ｐが垂直であることより 　{(p)-(a)}・{(p)+(a)}=0 下の式は、上の式を２乗すれば得られます。
	（２）ＡＰの長さがＯＡと等しいので、 　|(p)-(a)|=|(a)| または、左図のＯＰとＡ’Ｐが垂直であることより 　(p)・{(p)-2(a)}=0 下の式は、上の式を２乗すれば得られます。
	（３）ＢＰの長さがＡＢと等しいので、 　|(p)-(b)|=|(a)-(b)| または、左図のＡＰとＡ’Ｐが垂直であることより 　{(p)-(a)}・{(p)+(a)-2(b)}=0 下の式は、上の式を２乗すれば得られます。
	（４）ＡＰとＢＰが垂直であることより、 　{(p)-(a)}・{(p)-(b)}=0

「算数・数学」の部屋に戻る