多角形の面積

こちらのページより引用

多角形の各頂点が座標で表されているとき、その多面体の面積は次の式で計算できます。

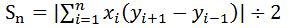　　（ただし　yn+1＝y1、y0＝yn）　　　・・・(1)


補題
　三角形Ａ1Ａ2Ａ3 が、Ａ1→Ａ2→Ａ3→Ａ1 が反時計回りの位置関係にあるとき、
三角形Ａ1Ａ2Ａ3の面積は　x1(y2-y3)＋x2(y3-y1)＋x3(y1-y2) で表される。
ただし、Ａ1：(x1, y1)、Ａ2：(x2, y2)、Ａ3：(x3, y3)

補題の証明
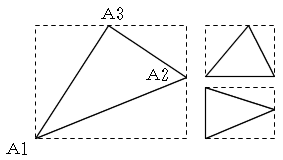
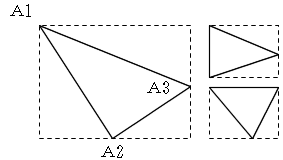
座標軸と三角形の関係は下のいずれかになります。
図の右に小さく描いたような状態、および、２辺がx軸、ｙ軸と平行な直角三角形も同様に計算できます。

図 面積の計算 図 面積の計算
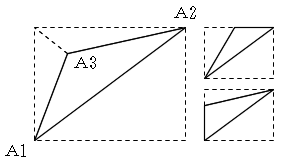
長方形の面積：(x2-x1)(y3-y1)
三角形の面積１：(x2-x1)(y2-y1)/2
三角形の面積２：(x2-x3)(y3-y2)/2
三角形の面積３：(x3-x1)(y3-y1)/2
以上より
△Ａ1Ａ2Ａ3の面積：
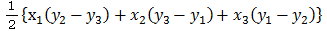 長方形の面積：(x2-x1)(y2-y1)
三角形の面積１：(x2-x1)(y2-y1)/2
三角形の面積２：(x2-x1)(y2-y3)/2
三角形の面積３：(x3-x1)(y2-y1)/2
以上より
△Ａ1Ａ2Ａ3の面積：
 
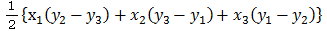長方形の面積：(x1-x3)(y2-y1)
三角形の面積１：(x1-x2)(y2-y1)/2
三角形の面積２：(x2-x3)(y2-y3)/2
三角形の面積３：(x1-x3)(y3-y1)/2
以上より
△Ａ1Ａ2Ａ3の面積：
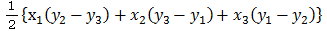 		 長方形の面積：(x3-x1)(y1-y3)
三角形の面積１：(x2-x1)(y1-y3)/2
三角形の面積２：(x3-x1)(y2-y3)/2
三角形の面積３：(x3-x1)(y1-y3)/2
以上より
△Ａ1Ａ2Ａ3の面積：
 
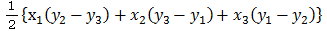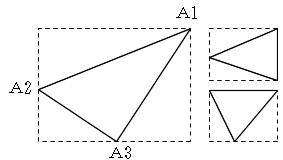長方形の面積：(x1-x2)(y1-y3)
三角形の面積１：(x1-x2)(y1-y2)/2
三角形の面積２：(x3-x2)(y2-y3)/2
三角形の面積３：(x1-x3)(y1-y3)/2
以上より
△Ａ1Ａ2Ａ3の面積：
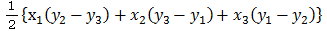 		  長方形の面積：(x2-x1)(y1-y2)
三角形の面積１：(x2-x1)(y1-y2)/2
三角形の面積２：(x2-x3)(y1-y2)/2
三角形の面積３：(x2-x1)(y1-y3)/2
以上より
△Ａ1Ａ2Ａ3の面積：
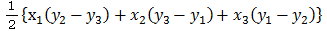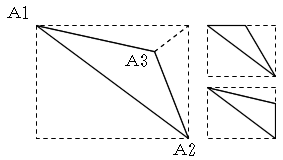
 長方形の面積：(x3-x1)(y1-y2)
三角形の面積１：(x2-x1)(y1-y2)/2
三角形の面積２：(x3-x2)(y3-y2)/2
三角形の面積３：(x3-x1)(y1-y3)/2
以上より
△Ａ1Ａ2Ａ3の面積：
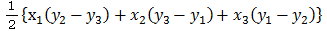 長方形の面積：(x3-x1)(y3-y1)
三角形の面積１：(x3-x1)(y2-y1)/2
三角形の面積２：(x3-x2)(y3-y1)/2
三角形の面積３：(x3-x1)(y3-y1)/2
以上より
△Ａ1Ａ2Ａ3の面積：
 

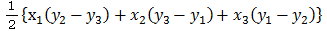以上より、補題は証明されました。


証明
ｎ＝３　のとき、補題により、式（１）は成り立ちます。

ｎ＝ｋ　（ｋは３以上の整数）のとき、式（１）が成り立つとする。つまり、
　Sk＝(1/2){x1(y2-yk)＋x2(y3-y1)＋・・・＋xk(y1-yk-1)}
このとき、辺ＡkＡ1 に、△ＡiＡkＡk+1 （この順に反時計回り）をくっつけて、ｋ＋１角形を作ることを考えます。

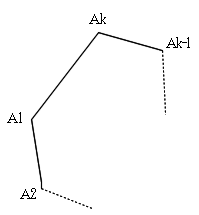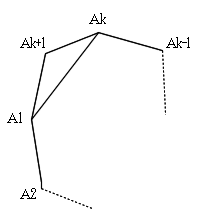
△ＡiＡkＡk+1 の面積は補題より、
　
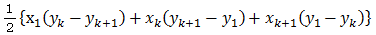
よって、
　Sk+1＝Sk＋(1/2){x1(yk-yk+1)+xk(yk+1-y1)+xk+1(y1-ｙk)}
　　＝(1/2){x1(y2-yk)＋x2(y3-y1)＋・・・＋xk(y1-yk-1)+x1(yk-yk+1)+xk(yk+1-y1)+xk+1(y1-ｙk)}
　　＝(1/2){x1(y2-yk+1)＋x2(y3-y1)＋・・・＋xk(yk+1-yk-1)+xk+1(y1-ｙk)}
よって、n=k+1 のときも、(1) は成り立ちます。

以上より、３以上の任意の整数ｎについて　（１）　が成り立ちます。

算数・数学の部屋に戻る