問題
t-1≦x≦t における関数 f(x)=2+2x-x2の最大値をM(t),最小値をm(t)とする。M(t)およびm(t)を求めよ。
解答
まず、y=f(x) のグラフは以下のようになります。頂点は(1,3) です。
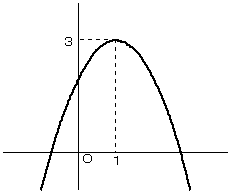
これを、幅が1の区間 t-1≦x≦t で切ると、その区間内の最大値、最小値は以下のようになります。
syoさんからの質問1
問題
t-1≦x≦t における関数 f(x)=2+2x-x2の最大値をM(t),最小値をm(t)とする。M(t)およびm(t)を求めよ。
解答
まず、y=f(x) のグラフは以下のようになります。頂点は(1,3) です。
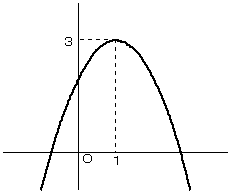
これを、幅が1の区間 t-1≦x≦t で切ると、その区間内の最大値、最小値は以下のようになります。
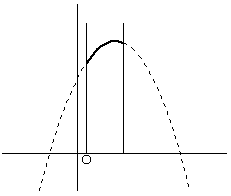
| t<1のとき | 1≦t<1.5のとき | t=1.5のとき |
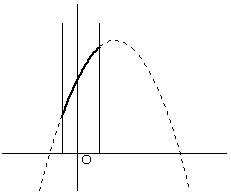 |
 |
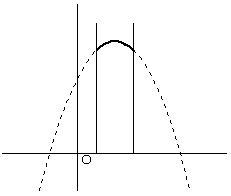 |
| x=t-1 で最小値 x=t で最大値 |
x=t-1 で最小値 x=1 で最大値 |
x=t-1 および x=t で最小値 x=1 で最大値 |
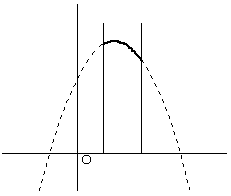
| 1.5<t≦2のとき | 2<t のとき | f(t-1)=-1+4t-t2 f(t)=2+2t-t2 より、以上をまとめると M(t)=2+2t-t2 (t<1) 3 (1≦t≦2) -1+4t-t2 (2<t) m(t)=-1+4t-t2 (t<1.5) 2+2t-t2 (t≧1.5) |
 |
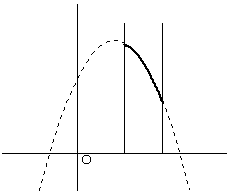 |
|
| x=t で最小値 x=1 で最大値 |
x=t で最小値 x=t-1 で最大値 |