問題
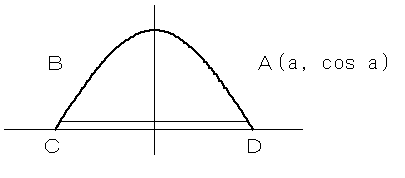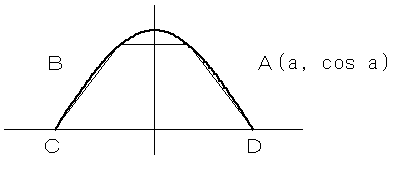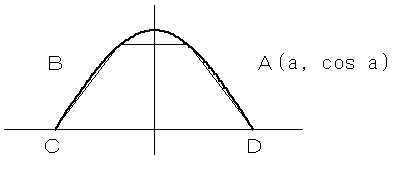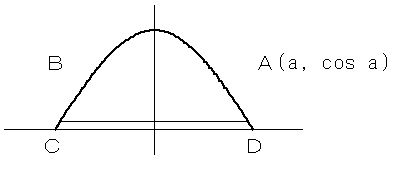
曲線:y=cosx (|x|≦π/2) とx軸に内接する台形ABCDを考える。
いま、台形ABCDを図のようにとり、点Aを、A(a,cosa)(0<a<π/2)と表す。
(1)台形ABCDの面積S(a)は最大値をとることを示せ。
(2)S(a)の最大値を与えるaの値をa[0]とするとき、π/12<a[0]<π/6
が成り立つことを示せ。
解答
(1)
AB=2a
CD=π
より、台形ABCDの面積S(a)は、
S(a)={(2a+π)cosa}/2
と書けます。aで微分して、
S’(a)={2cosa−(2a+π)sina}/2
さらに微分して、
S”(a)={−2sina−2sina−(2a+π)cosa}/2
={−4sina−(2a+π)cosa}/2
0<a<π/2 の範囲では、
sina>0
cosa>0
2a+π>0
であるので、この範囲では常に
S”(a)<0
となり、S’(a) は、この範囲で、単調減少します。
a=0、a=π/2 においてS(a)および、S’(a) を定義しても、連続性は失われない。
S’(0)=1
S’(π/2)=−π
となり、S’(a) は、0<a<π/2 において連続であるので、
S’(a)=0
となるaが、この範囲内に1つ存在する。
それを a[0] とすると、単調性より
0<a<a[0] では、S’(a)>0
a[0]<a<π/2では、S’(a)<0
となり、S(a) は、a=a[0] で、極大かつこの範囲での最大となります。
(2)
同様に、
S’(π/12)={2cos(π/12)−(7π/6)sin(π/12)}/2
=(√6+√2)/4−(7π/6)(√6−√2)/8
≒(2.45+1.41)/4−7×3.14×(2.45−1.41)/48
=3.86/4−7×3.14×1.04/48
≒0.965−0.476
=0.489>0
S’(π/6)={2cos(π/6)−(4π/3)sin(π/6)}/2
=√3/2−(π/3)
≒1.73/2−3.14/3
≒0.865-1.047
=−0.182<0
以上より、S(a) を最大にするa[0] は、π/12<a[0]<π/6 の範囲内にあります。
「算数・数学」の部屋に戻る