問題
平面上の領域A,Bをそれぞれ
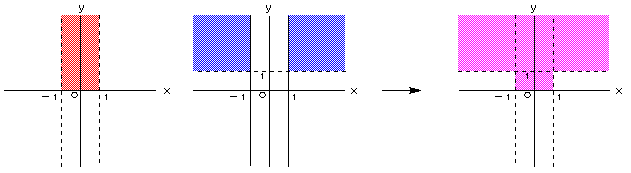
A={(x,y)||x|<1 かつ y>0} , B={(x,y)||x|≧1かつy>1}
とし、D=A∪Bとする。
i,領域Dを図示せよ。
ii,放物線y=-x2+2ax+bがDと交わらないためのa,bの条件を求めよ。また、そのような点(a,b)の存在する範囲を図示せよ。
解答
i. 下図の通り、ただし境界上の点は含まない。
ii.
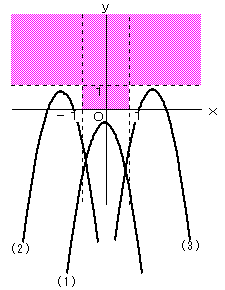
y=-x2+2ax+b は上に凸のグラフですが、これが領域Dと交わらないためには、上図のように
(1) 判別式≦0
判別式>0のとき、-x2+2ax+b=0 の2解を、α、β(α<β)とするとき、
(2) β≦−1 かつ 頂点のy座標≦1
(3) α≧1 かつ 頂点のy座標≦1
の、いずれかであればよい。
判別式/4=a2+b
α=a - √(a2+b)
β=a + √(a2+b)
頂点の座標(a, a2+b)
より、
(1) a2+b≦0
(2) a2+b>0 かつ a + √(a2+b)≦−1 かつ a2+b≦1
(3) a2+b>0 かつ a - √(a2+b)≧1 かつ a2+b≦1
●a + √(a2+b)≦−1
より、
√(a2+b)≦-(a+1)
0<√(a2+b) より、両辺2乗して
a2+b≦a2+2a+1
b≦2a+1
0<-(a+1) より、
a<-1
●a - √(a2+b)≧1
より、
√(a2+b)≦a - 1
0<√(a2+b) より、両辺2乗して
a2+b≦a2-2a+1
b≦-2a+1
0<a - 1 より、
a>1
以上より、
(1) b≦−a2
(2) 0<a2+b≦1 かつ b≦2a+1 かつ a<-1
(3) 0<a2+b≦1 かつ b≦-2a+1 かつ a>1
(1) または (2) または (3) で表される領域が求める領域であり、下図のようになります。
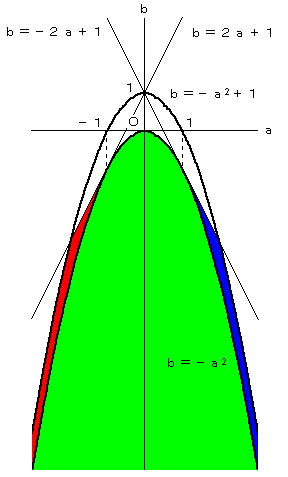
緑が (1) の領域、赤が (2) の領域、青が (3) の領域です。
実際の解答には色分けする必要はありません。
「算数・数学」の部屋に戻る