問題
y=x2とy=2x+15のグラフが2点A,Bで交わりy=x2上を原点Oから出発し、点Bまで動く点Pがある。
(1)点Pのx座標が2のとき、三角形APBの面積を求めよ。
(2)直線y=-2x-1とy=x2の交点を求めよ。
(3)点PがOからBまで動くとき三角形APBの面積の値が自然数となるような点Pは何個あるか。
解答
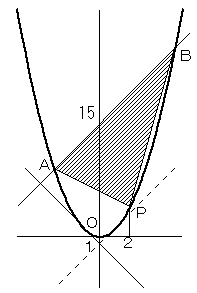
(1)
y=x2 と y=2x+15 を連立させて解くと、A,Bの座標は、
A:(−3,9)、B:(5,25)
また、P:(2,4)
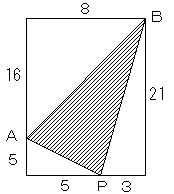
図より、△ABPの面積を求めると、
21×8−3×21÷2−5×5÷2−8×16÷2=60
(2)
y=-2x-1とy=x2 を連立させて、
x2+2x+1=0
(x+1)2=0
x=-1 (重解)
y=1 よって、求める交点は(−1,1)
(3)
(2) の結果より、y=-2x-1 は、y=x2 に接するが、対称性より、
y=2x-1 も y=x2に接する。
つまり、Pが(1,1) であるときが、△ABPの面積は最大であり、
(ABを底辺としたとき、点PがABからもっとも離れる位置)
そのときの面積は、図より、64(計算は省略)
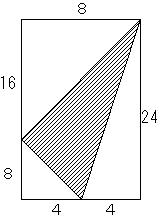
一方、点Pが原点にあるとき、△ABPの面積は、60
点PがOからBまで動くとき、面積は連続的に変化するので、
面積が自然数になるのは、点Oから点Pまで、
60, 61, 62, 63, 64
と増え、以下、点Bに至る直前まで、
63, 62, 61, ・・・ 1
と変化する。
よって、求める個数は、
5+63=68(個)
算数・数学の部屋に戻る