問題
(1)8x≡7(mod19)を満たすxの値を求めよ。
(2)31x≡2(mod13)を満たすxの値を求めよ。
(3)pが3より大きい素数のとき、p2-1は24の倍数であることを、合同の考えを用いて証明せよ。
解答
(1)
x≡0 (mod 19) のとき、8x≡8×0≡0 (mod 19)
x≡1 (mod 19) のとき、8x≡8×1≡8 (mod 19)
x≡2 (mod 19) のとき、8x≡8×2≡16 (mod 19)
x≡3 (mod 19) のとき、8x≡8×3≡24≡5 (mod 19)
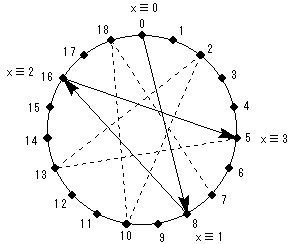
これは、図のような円を19等分した図で、点を8つずつ増やしながら
選んでいくのと同じ変化をします。
19 と 8 は互いに素なので、19 回目で初めて元の位置に戻り、8x≡7 (mod 19)
となるのは、
x≡8 (mod 19) のときだけである。
よって、x は、x=19n+8 (n は整数) となる数
(2)
31≡5 (mod 13) なので、
5x≡2 (mod 13) と置き直しても良い。
(1) と同様に考えると、
x≡3 (mod 13) のとき、5x≡2 (mod 13) なので、
x=13n+5 (n は整数) となる数
(3) 出題者の意図するような解答が思いつきませんが、とりあえず
合同式を使った解き方として。
p2−1=(p−1)(p+1)
pは2で割り切れないので、
p−1≡0、p+1≡2 (mod 8) このとき (p−1)(p+1)≡0 (mod 8)
または p−1≡2、p+1≡4 (mod 8) このとき (p−1)(p+1)≡8≡0 (mod 8)
または p−1≡4、p+1≡6 (mod 8) このとき (p−1)(p+1)≡24≡0 (mod 8)
または p−1≡6、p+1≡0 (mod 8) このとき (p−1)(p+1)≡0 (mod 8)
よって、いずれの場合も (p−1)(p+1)≡0 (mod 8)
pは3で割り切れないので、
p−1≡1、p+1≡0 または p−1≡0、p+1≡2 (mod 3)
であり、いずれの場合も、(p−1)(p+1)≡0 (mod 3)
以上より、 p2−1 は8でも3でも割り切れるので、24の倍数である。
算数・数学の部屋に戻る