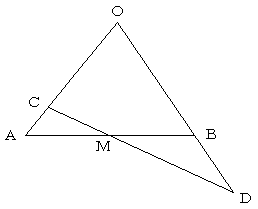
問題
△OABにおいて、辺OAを3:1に内分する点をC,辺ABの中点をMとする。
またOA=a,OB=bとする。
1.OCをaを用いて表せ。また,CMをa,bを用いて表せ
2.直線CMと直線OBの交点をDとする。OD=kbとおく時、
実数kの値を求めよ。
3.OA=3,OB=5,線分CMの中点をNとする。2.の点Dに対して,
ON⊥CDが成り立つ時、cos∠AOBの値を求めよ。
解答
1.
OCはaと同じ向きのベクトルで、長さが3/4倍なので、
OC=3a/4 ・・・答え
MはABの中点なので、
OM=(a+b)/2
CM=OM−OC=(a+b)/2−3a/4=b/2−a/4 ・・・答え
2.
CD=OD−OC=kb−3a/4
一方、CMはCDと同じ向きのベクトルなので、ある実数tに対して
CD=tCM
とおけます。これより、
kb−3a/4=t(b/2−a/4)
aとbは平行でないので、それぞれの係数を比較して、
−3/4=−t/4
k=t/2
以上より、
t=3,k=3/2 ・・・答え
3.
NはCMの中点なので、
ON=(OC+OM)/2={3a/4+(a+b)/2}/2=5a/8+b/4
これと、
CM=b/2−a/4
とが垂直なので、内積を取って、
ON・CM=(5a/8+b/4)・(b/2−a/4)
=(5a+2b)・(2b−a)/32=0
(5a+2b)・(2b−a)=−5a・a+4b・b+8a・b
=−5|a|2+4|b|2+8|a||b|cos∠AOB=0
|a|=3、|b|=5 より、
−5・32+4・52+8・3・5cos∠AOB=55+120cos∠AOB=0
よって、
cos∠AOB=−55/120=−11/24・・・答え
「算数・数学」の部屋に戻る