問題1
円C1:x2+y2-2x-4y-4=0が、円C2:x2+y2-2y+1-a=0と接するような定数aの値を求めたい。
このとき、次の各問いに答えよ。
(1)円C1の中心の座標と半径を求めよ。
(2)円C1が円C2と接するような定数aの値を求めよ。
問題2 円x2+y2=5上の点(1,2)でこの円と接するような直線の方程式を求めよ。
解答1
(1)
x2+y2-2x-4y-4=0 を変形して、
(x-1)2+(y-2)2=9=32
よって、中心:(1,2)、半径:3
(2)
x2+y2-2y+1-a=0 を変形して、
x2+(y-1)2=a
より、a>0であり、C2は、中心:(0,1)、半径√a
よって、円C1と円C2の中心距離は
√{(1-0)2+(2-1)2}=√2
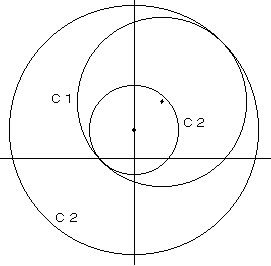
C2がC1に接するのは、
√2+√a=3 または √2+3=√a
よって、
√a=3±√2
a=(3±√2)2=11±6√2
解答2