問題
直角三角形ABCの斜辺BC上を点Pが動く。
Pから辺AB,ACに 垂線PQ,PRを引く。
このとき△PRQの面積を最大にする点Pの位置を 求めよ。
解答
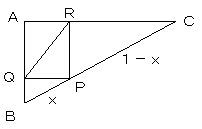
△PRQが最大のときは、長方形AQPRが最大であり、すなわち
△QBP+△RPCの和が最小のときです。
BP:PC=x:(1−x) (0≦x≦1) とします。
△ABC、△QBP、△RPC は相似であり、△ABCの面積をSとすると、
△QBP=Sx2
△RPC=S(1−x)2
よって、
x2+(1−x)2
が最小となる x を見つければいいことになります。
x2+(1−x)2=2x2−2x+1
=2(x−1/2)2+1/2
となり、x=1/2 のとき、最小値 1/2 をとります。
答え PがBCの中点であるとき
「算数・数学」の部屋に戻る