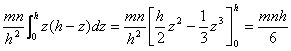ロダンさんからの質問１

問題１
　ねじれの位置にある直線P,Q上に一定の長さの線分AB,CDを取るとき、
四面体ABCDの体積は一定であることを示せ。

解答１

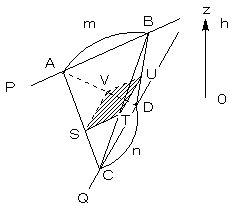
ＡＢ＝ｍ、ＣＤ＝ｎ とします。
図のようにＰともＱとも垂直な方向に ｚ軸をとり、ＰとＱの距離をｈとします。
ｚ軸に垂直で、Ｑからｚだけ離れた平面で、四面体ＡＢＣＤを切った切り口を
ＳＴＵＶとすると、ＳＴとＵＶはＰに平行で、ＴＵとＳＶはＱに平行なので、
四角形STUVは平行四辺形であり、
　TU＝ＳＶ＝ｎ(ｚ／ｈ)
　ＳＴ＝ＵＶ＝ｍ{(ｈ−ｚ)／ｈ}
また、ＳＴとＴＵのなす角は、
ＰとＱのなす角なので、一定です。これをθとします。

平行四辺形STUVの面積Ｓ(z) は、
　Ｓ(z)＝ＳＴ・ＴＵsinθ＝mnz(ｈ−ｚ)/ｈ²
これを、ｚ＝０からｚ＝ｈまで積分したものが、四面体ＡＢＣＤの体積であるので、
四面体ＡＢＣＤの体積はABおよびＣＤの位置にかかわらず一定である。

ちなみに、体積を求めると、

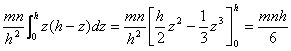
となります。

問題２
　直線（x-1)/2=-y-1=(z-3)/4の平面x+2y+z=6への正射影の方程式を求めよ。

解答２

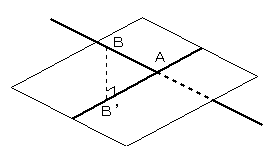
図のように、直線と平面の交点をＡ、Ａ以外の直線上の点Ｂから、
平面におろした垂線の足をＢ’とすると、ＡＢ’が求める直線になります。

　（x-1)/2=-y-1=(z-3)/4＝ｔ
とおくと、この直線上の任意の点は
　ｘ＝２ｔ＋１
　ｙ＝−ｔ−１
　ｚ＝４ｔ＋３
で表せます。これを、x+2y+z=6 に代入して、
　(2t+1)+2(-t-1)+(4t+3)＝6
　ｔ＝１
よって、点Ａの座標は、(3, -2, 7)。

次に、点Ｂとして、(1, -1, 3) をとります。
ＢＢ’は平面 x+2y+z=6 に垂直なので、方向ベクトルは、(1, 2, 1)。
ＢＢ’上の点は、
　ｘ＝ｔ＋１
　ｙ＝２ｔ−１
　ｚ＝ｔ＋３
と表せます。これを、x+2y+z=6 に代入して、
　(t+1)+2(2t-1)+(t+3)＝6
　ｔ＝2/3
よって、Ｂ’の座標は (5/3, 1/3, 11/3)

AB'の方向ベクトルは、(3, -2, 7)−(5/3, 1/3, 11/3)＝(4, -7, 10)/3
よって、AB'を表す式は、以下のように書けます。
　(x-3)/4＝-(y+2)/7＝(z-7)/10

算数・数学の部屋に戻る