問題
定義域がx≧0である4つの関数がある。
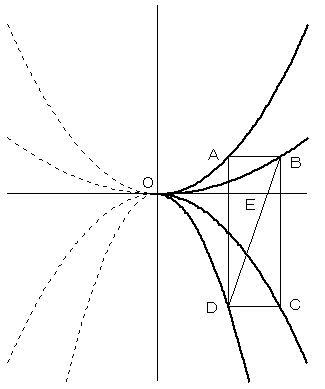
今、4点 A、B、C、Dはそれぞれ関数(1)−(4)のグラフ上にあって、
ABとDCはx軸に平行、BCとADはy軸に平行である。
点Aのx座標をa、原点をOとするとき、次の各問に答えよ。
y=x2---(1)
y=(x2)/3--(2)
y=-x2--(3)
y=kx2--(4)
(1)kの値を求めよ。
(2)四辺形ABCDが正方形になるときのaの値を求めよ。
(3)BDとx軸との交点をEとし、三角形AEBの面積が4(√3-1)であるときのaの値と三角形OEDの面積を求めよ。
解答
題意より、四角形ABCDが長方形であることはすぐわかる。
Aの座標を(a、a2)とおくと、Bのy座標も a2なので、このときBのx座標xbは
a2=(xb2)/3
より、xb=√3a 。さらに、Cのx座標も √3a なので、Cのy座標ycは
yc=-(√3a)2=-3a2
よって、Dの座標は(a、-3a2)であり、y=kx2---(4) がこの点を通るためには、
-3a2=ka2
a>0より、k=-3 ・・・(1)の答え
AB=√3a-a=(√3-1)a
BC=a2-(-3a2)=4a2
四辺形ABCDが正方形になるためには、AB=BC となればいいので、
(√3-1)a=4a2
a>0より、a=(√3-1)/4 ・・・(2)の答え
△AEBの面積は
AB×ya÷2=(√3-1)a×a2÷2=4(√3-1)
より、a3=8
aは実数なので、a=2 ・・・(3)の答え1
このとき、Bの座標:(2√3、4)、Dの座標:(2、-12)より、
BDの直線の式は、
y=16(x-2)/(2√3-2)-12
y=8(x-2)/(√3-1)-12
y=0とすると、
0=8(x-2)/(√3-1)-12
8(x-2)/(√3-1)=12
x-2=3(√3-1)/2
x=(3√3+1)/2
より、Eの座標:((3√3+1)/2, 0)
△OEDの面積は、
(3√3+1)/2×12÷2=3(3√3+1)=9√3+3 ・・・(3)の答え2
算数・数学の部屋に戻る