冷凍ビームさんからの質問１

問題
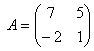　とする。Ａの固有値がλ＝ａ＋ｂｉ と共役複素数 λ’であるとき、ａ、ｂを求めよ。ただし、ｂ＞０とする。

また、 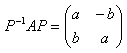が、 を満たすとき、行列Ｐを求めよ。

解答
固有値の性質より、が、逆行列を持たないことが、必要条件であるので、行列式を取って、
　(７−λ)(１−λ)−５・（−２）＝０
　λ²−８λ＋１７＝０
これを解いて、
　λ²−８λ＋１６＝−１
　(λ−４)²＝−１
　λ＝４±ｉ
よって、ａ＝４，ｂ＝１

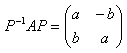を変形して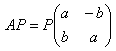　
よって、

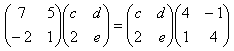
これを、成分別に計算すると、
　７ｃ＋１０＝４ｃ＋ｄ　・・・(1)
　７ｄ＋５ｅ＝−ｃ＋４ｄ　・・・(2)
　−２ｃ＋２＝ｅ＋８　・・・(3)
　−２ｄ＋ｅ＝４ｅ−２　・・・(4)
(1)より
　ｄ＝３ｃ＋１０　・・・(1)’
(2) を移項した ３ｄ＋ｃ＋５ｅ＝０ に代入して
　１０ｃ＋３０＋５ｅ＝０
　ｅ＝−２ｃ−６　・・・(2)’
(1)’(2)’ は、恒等的に(3)(4) を満たすので、これらは、１次独立ではなく、
解は一意に決まりません。
つまり、

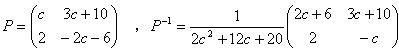
の形の行列であれば、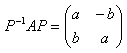を満たします。

算数・数学の部屋に戻る