問題
座標平面上の4点(0,0)(1,0)(1,1)(0,1)を頂点とする正方形の周および内部をFとする。
Fと放物線y=(x-a)2+bが共有点をもつための実数a,bの条件を求めよ。
解答
まず、放物線 y=(x-a)2+b は下に凸で、頂点は(a, b) です。
頂点がFの中にある時は、当然条件を満たします。よって、
0≦a≦1 かつ 0≦b≦1
それ以外の場合で、共有点を持つのは、下図のような場合です。
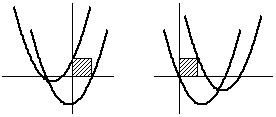
つまり、 f(x)=(x-a)2+b
とおくとき、
f(0)≦1 かつ f(1)≧0 (左図)
または
f(0)≧0 かつ f(1)≦1 (右図)
a,b の式で表すと、
a2+b≦1 かつ (a-1)2+b≧0
または
a2+b≧0 かつ (a-1)2+b≦1
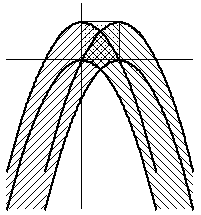
これらを図示すると、以下のようになります。
横軸a、縦軸b で、正方形の1辺は1です。
算数・数学の部屋に戻る