問題
一辺の長さが√2cmの正四面体P−QRSの4頂点を中心とし、
半径がすべて r cm に等しい球がある。
さらにその4つの球に外接する球Oがあって、この球Oの半径もまた r cmである。
この r の大きさを立方体を用いて求めたい。
(1)立方体ABCD−EFGHの適当な4頂点を結んで正四面体の見取り図を作る事が出来る。
1頂点をAとするとき正四面体の見取り図をかけ。
(2) (1)で作った正四面体が正四面体PQRSと合同であるとき、立方体ABCD−EFGH
の一辺の長さを求めよ。
(3)球の中心を考えて r を求めよ。
解答
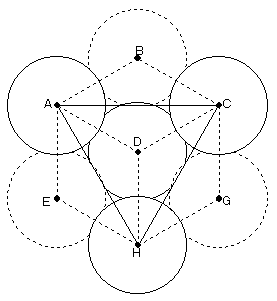
(1) 正方形から、4つの三角錐を切り取って、正四面体を作る図は、
作り散らかした画像集の中にあるので、それに適当にABC・・・を付ければ出来上がりです。
(2)このとき、正四面体の1辺は、元の立方体の1つの面の対角線になっており、
それが√2 cm なので、立方体ABCD−EFGHの1辺は1 cm。
(3)つまり、この立方体で、正四面体の頂点にならなかった頂点を中心にして、
半径 r cm の球を置いても、やはり中心の球と接する。
下図において、実線が正四面体の頂点および中心を中心とする球。
破線が、それ以外の立方体の頂点を中心とする球。図では、点Dを中心とする球(破線)
は描いていない。また、隠れて見えないが、点Fを中心とする球(実線)がある。
ここで、中心をOとすると、立方体の対角線(例えば、CE)の中点が点Oであり、3点C、O、E
を中心とする球は図のように、接しながら、一直線上に並ぶ。
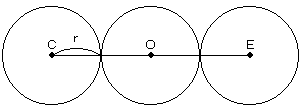
CEの長さは√3 cm なので、球の半径 r は
r=√3/4
「算数・数学」の部屋に戻る