雷同さんからの質問１

問題
放物線 y=ax² と、点Ａ（−６、０）を通る直線が、２点Ｂ，Ｃで交わっており
　ＡＢ：ＡＣ＝１：４
である。２点Ｂ、Ｃのx座標をそれぞれ求めよ。

解答

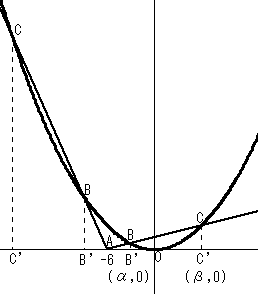
点Ａ、Ｂ、Ｃの位置関係は上の図のようになります。（点Ｂ、Ｃの候補となる位置は点Ａに対して
左右２通りあります。ただし、最初から２通りあることに気がつく必要はありません。）
点Ｂ、Ｃから ｘ軸におろした垂線の足を点Ｂ’、Ｃ’ とすると、
　ＡＢ’：ＡＣ’＝ＡＢ：ＡＣ＝１：４ です。
ここで、点Ｂ’：（α、０）、点Ｃ’：（β、０） とおくと、α、βが求めるｘ座標になります。
一方、点Ａ（−６，０）を通る直線で、ｙ軸に垂直な直線 ｘ＝−６ は、条件に合わないことが明らか
なので、それ以外の直線はすべて
　ｙ＝ｍ（ｘ＋６）
で表されます。よって、連立方程式
　ｙ＝ａｘ²　・・・(1)
　ｙ＝ｍ（ｘ＋６）　・・・(2)
の解が点Ｂ、Ｃとなります。
(1),(2) より、ｙを消去して、
　ａｘ²−ｍｘ−６ｍ＝０
これの２解がα、βなので、解と係数の関係より
　α＋β＝ｍ/ａ　・・・(3)
　αβ＝−６ｍ/ａ　・・・(4)
また、ＡＢ’：ＡＣ’＝１：４　より、
　β＋６＝４（α＋６）
変形して
　β＝４α＋１８　・・・(5)
(3)(4) より、
　αβ＝−６（α＋β）
(5) を代入して
　α（４α＋１８）＝−６（５α＋１８）
　４α²＋４８α＋１０８＝０
　α²＋１２α＋２７＝０
これを解いて、
　α＝−３，−９
(5) よりβを求めると
　（α、β）＝（−３，６）または（−９，−１８）
答え　点Ｂ、点Ｃのｘ座標は、−３と６　または　−９と−１８

「算数・数学」の部屋に戻る