通常、直角を 90°と言ったり、三角形の内角の和は 180°であると
言ったりする場合の角度の単位 (°) は、一周を 360°として決められた
ものです。
360 という数は、約数が多いとか、1年365日に近いので、天体や暦に便利とか
それなりの長所はありました。
一方、それとは別の角度の単位(rad:ラジアン)というものが定義されました。
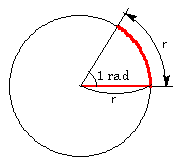
半径 r の円から、弧の長さが半径と同じ r になる扇形を考えます。
このときの中心角を 1rad(ラジアン)と決めます。(日本語では1弧度といいます)
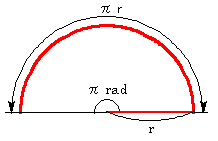
すると、半円の弧の長さはπr ですから、このときの弧の長さは1rad のときの
π倍になっています。中心角と弧の長さは比例しますから、ここで、
180°=π rad
という関係があることが分かります。
ちなみに、1rad は約 57.295…° ですが、このことはさして重要でなく、
180°=π rad
であることが、もっとも覚えておかなければならない、度とrad の換算式です。
以後、rad という単位は省略して、角度に何も単位がついていなければ rad
であるという、暗黙の了解があります。
このような角度の表し方を弧度法といいます。
さて、弧度法を使うことにより何が変わるかというと、例えば、扇形の弧の長さや
面積を求める式が以下のように変わります。
半径 r 、中心角d°=θ rad の扇形について、