問題
2次方程式 x^2-2tx+t^2-3t=0 の異なる解がともに0より大きくなるように、定数tの値の範囲を求めた。
次のア〜ケをうめよ。ただし*には>、<、≧、≦のいずれかを入れよ。
f(x)=x^2-2tx+t^2-3tとおく。
頂点の座標は(ア,イ)
異なる2つの解が、ともに0より大きくなる条件は、グラフが下に凸より、
・頂点のy座標(*ウ)0より、t>エ
・頂点のx座標(*オ)0
・f(0)(*カ)0より、t<キまたはク<t
が成り立つことである。
よって、求める定数tの値の範囲はケ<tである。
解答
グラフはこのようになります。
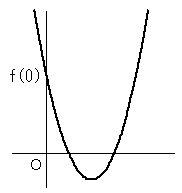
f(x)=x^2-2tx+t^2-3t
を変形して
f(x)=(x-t)^2-3t
よって、頂点の座標は (t,-3t) ・・・(ア)(イ)
異なる2つの解が、ともに0より大きくなる条件は、グラフが下に凸より、
・頂点のy座標<0より、t>0 ・・・(ウ)(エ)
・頂点のx座標>0 ・・・(オ)
・f(0)>0より、 ・・・(カ)
f(0)=t^2-3t=t(t-3)>0
よって、
t<0または3<t ・・・(キ)(ク)
よって、求める定数tの値の範囲は3<tである。 ・・・(ケ)
このような、穴埋めでない場合は、次のようにしても解けます。
f(x)=x^2-2tx+t^2-3t
の解をα、β とすると、解と係数の関係より
α+β=2t、αβ=t^2-3t
α、βともに正であるには、α+β>0 かつ αβ>0 が必要。つまり、
2t>0 かつ t^2-3t>0
また、判別式を取って、
D/4=3t>0
以上より、求める範囲は、3<t となります。
算数・数学の部屋に戻る