質問
縦横比と回転角の異なる2つの長方形の、片方の図形上の任意の点に対応するもう片方の
点の座標を求める式が知りたいのです。
どういう座標を与えれば良く、どのような計算式になるのでしょうか?
回答
問題を、以下のように理解しました。
文系のもうりぃ さんからの質問
質問
縦横比と回転角の異なる2つの長方形の、片方の図形上の任意の点に対応するもう片方の
点の座標を求める式が知りたいのです。
どういう座標を与えれば良く、どのような計算式になるのでしょうか?
回答
問題を、以下のように理解しました。

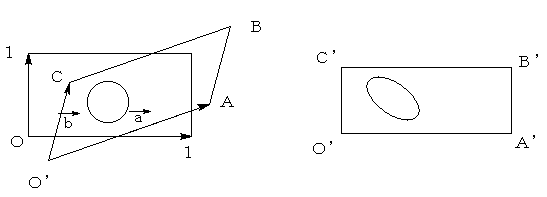
上図左の長方形上に円が描かれている。
これを右の長方形を通して見ると、図のように楕円のようにゆがんで見える。
座標系がちがうからだ。
そこで、左の長方形(Aとする)の左下を原点とし、辺の方向にx軸、y軸をとる。
ここでは、便宜上、長方形の1辺を1としたが、任意の値を設定してもかまわない。
もう一つの長方形(Bとする)の4つの頂点が、長方形Aで設定した座標では、どの位置に
当たるかを調べる。それらを、O'、A,B,C
とする。
四角形O'ABCは、平行四辺形であるのが普通で、それ以外の場合は、複雑な計算が必要になる。
※長方形、正方形、ひし形も平行四辺形である。一般の台形やその他の四角形は不可。
※※以下、太字はベクトルを表す。
O'A=a、O'C=b とおく。
長方形Aで設定した座標での任意の点Pについて、
O'P=sa+tb
で表せるような、実数s、t を求めることができ、この
s、t が長方形B上での座標ということになる。
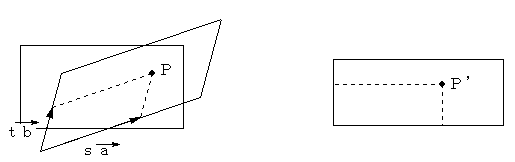
今、O'P=(x、y)、a=(ax、ay)、b=(bx、by) とすると、
x=sax+tbx
y=say+tby
となり、このs、t についての連立方程式を解けばいいことになる。